こんにちは。福田泰裕です。
高校の数学で学習する、正多面体を覚えていますか?
今回は、この正多面体が5種類しか存在しないことのエレガントな証明をご紹介します。
最後まで読んでいただけると嬉しいです。
目次
正多面体は5種類しか存在しない
まず、正多面体について説明します。
正多面体とは、
① すべての面が同一の正多角形で構成され、
② すべての頂点において接する面の数が等しい、
③ 凸多面体
のことです。
つまり、正多面体を構成する正多角形の辺の数と、頂点にあつまる面の数が決まれば、正多角形が1つに決まるということです。
正多面体を構成する面が正 \(p\) 角形、1つの頂点に集まる面の数を \(q\) とすると、正多面体は
\((p,q)\)
のように表すことができます。
(この数を「シュレーフリ記号」と呼びます。)
そしてこの正多面体は、正四面体、正六面体、正八面体、正十二面体、正二十面体の5つしか存在しないことが分かっています。
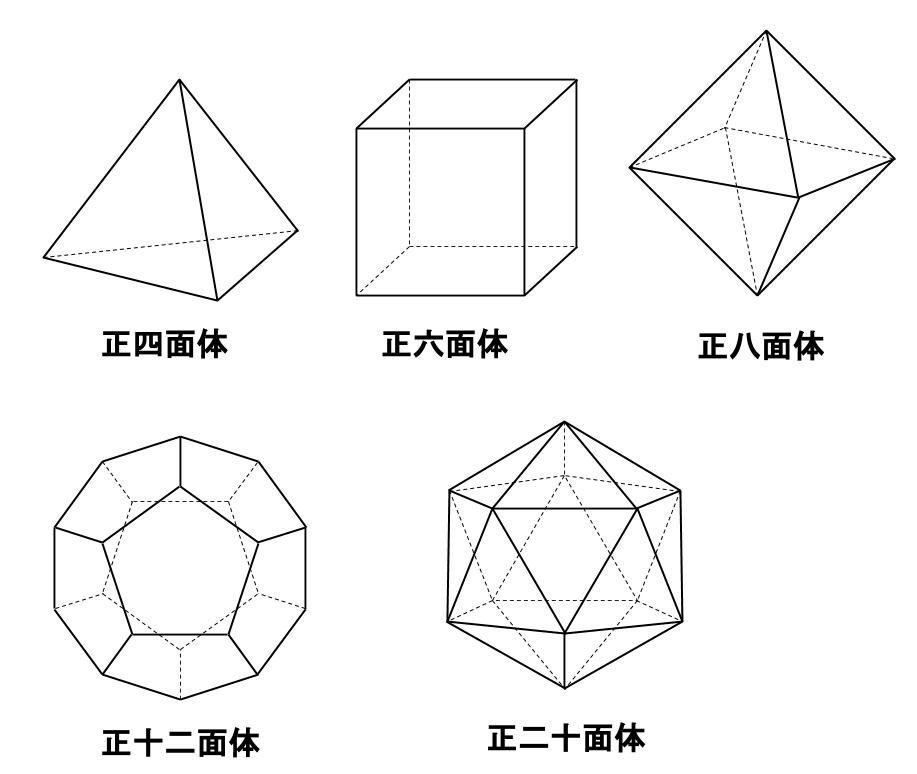
シュレーフリ記号を使うと、
- 正四面体は \((3,3)\)
- 正六面体は \((4,3)\)
- 正八面体は \((3,4)\)
- 正十二面体は \((5,3)\)
- 正二十面体は \((3,5)\)
と表されます。
直観では、

えっ、5種類?
もっとありそうだけど…
と思いませんか?
それでは、正多面体が5種類しか存在しないことのエレガントな証明を見ていきましょう。
正多面体が5種類しか存在しないことのエレガントな証明
この証明では、正多面体の展開図を考えます。
ここで、立体を構成するためには、1つの頂点に集まる面の数は3以上でなければなりません。
(頂点にあつまる面の数が2だと、山折りできるだけで立体にはならない。)
また、1つの頂点に集まる角の和が360°未満でなければ展開図が描けません。
この2つの事実を使い、証明を進めていきましょう。
正多面体を “正三角形” で構成する場合
まず、正三角形 \((p=3)\) で構成する場合を考えます。
正三角形の内角は60°です。
「1つの頂点に集まる面の数は3以上」かつ「1つの頂点に集まる角の和が360°未満」であるためには、\(q=3,4,5\) であることが必要です。
(\(q \geq 6\) だと、360°以上になってしまうので不適。)
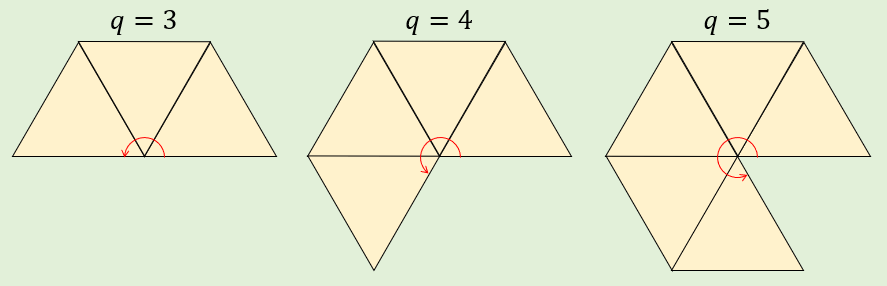
よって、\(p=3\) のとき、
\((3,3),(3,4),(3,5)\)
の3種類となります。
正多面体を “正四角形” で構成する場合
次に、正四角形 \((p=4)\) で構成する場合を考えます。
正三角形の内角は90°です。
「1つの頂点に集まる面の数は3以上」かつ「1つの頂点に集まる角の和が360°未満」であるためには、\(q=3\) でなければなりません。
(\(q \geq 4\) だと、360°以上になってしまうので不適。)
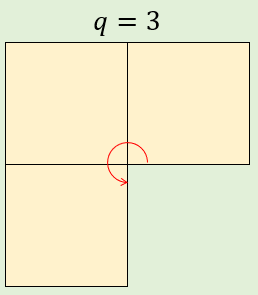
よって、\(p=4\) のとき、
\((4,3)\)
の1種類のみとなります。
正多面体を “正五角形” で構成する場合
次に、正五角形 \((p=5)\) で構成する場合を考えます。
正三角形の内角は108°です。
「1つの頂点に集まる面の数は3以上」かつ「1つの頂点に集まる角の和が360°未満」であるためには、\(q=3\) でなければなりません。
(\(q \geq 4\) だと、360°以上になってしまうので不適。)
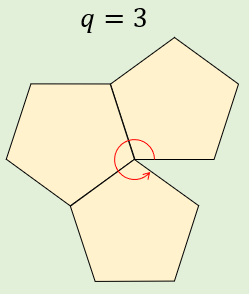
よって、\(p=5\) のとき、
\((5,3)\)
の1種類のみとなります。
正多面体を “正六角形” で構成する場合
この調子で、正六角形 \((p=6)\) で構成する場合も考えてみましょう、
正六角形の内角は120°です。
「1つの頂点に集まる面の数は3以上」なので \(q=3\) から考えますが…
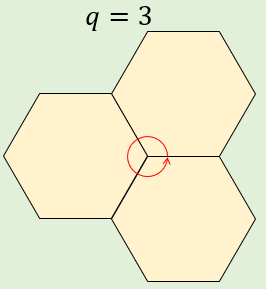
これだと、「1つの頂点に集まる角の和が360°未満」という条件を満たしていません。
ぴったり360°だと、立体を構成することができません。
つまり、正六角形 \(p=6\) のとき、条件を満たす \(q\) は存在しないことになります。
更にこれから先を考えると、\(p\) が大きくなると内角も大きくなります。
よって、\( p \geq 7\) だと \(q=3\) でも360°を超えてしまうので、条件を満たす \(q\) は存在しないことになります。
故に、\(p \geq 6\) のとき、条件を満たす \(q\) は存在しません。
以上から、条件を満たすのは、
\((p,q)=(3,3),(3,4),(3,5),(4,3),(5,3)\)
の5種類のみであることが証明できました。
まとめ:正多面体が5種類しか存在しないことは2300年以上前に分かっていた
いかがでしたでしょうか。
正多面体が5種類しか存在しないことは直観に反していますが、このように証明されました。
しかし驚くべき事に、この正多面体が5種類しか存在しないことは、紀元前3世紀頃に書かれたユークリッドの『原論』に記されています。
今から2300年以上前にすでに分かっていたなんて、驚きですよね…。
高校の授業でこの証明まで習うことは少ないかもしれませんが、ぜひ展開図を用いたエレガントな証明にも触れて、数学の面白さを知ってもらいたいです。
この多面体を語るうえで重要な「オイラーの多面体定理」というものがあります。
高校数学で学習しますが、ほとんど入試で出題されないために忘れられている定理です。
しかし、このオイラーの多面体定理もエレガントな証明があるので、ぜひご覧ください👇
最後まで読んでいただき、ありがとうございました!
質問やご意見、ご感想などがあればコメント欄にお願いします👇




コメント