こんにちは。福田泰裕です。
この記事では、2021年日本数学オリンピック(JMO)第2問の問題を解説していきます。
最後まで読んでいただけると嬉しいです!
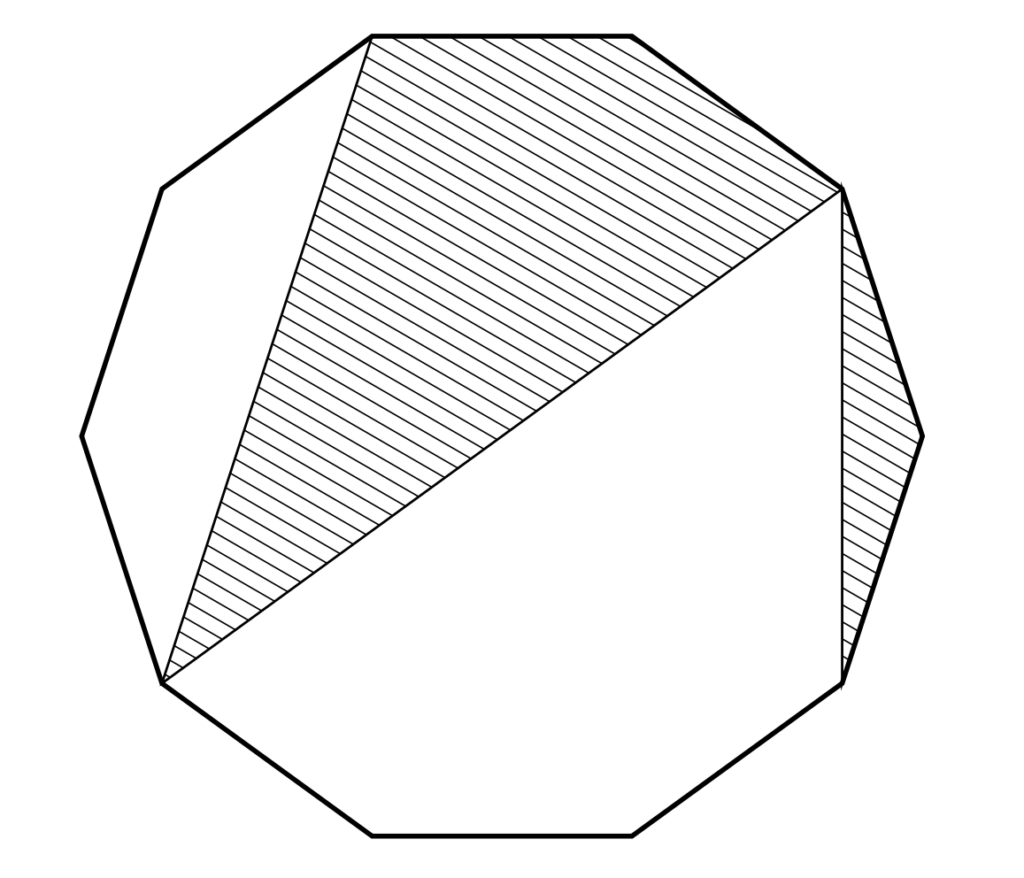
【日本数学オリンピック(JMO)予選2021第2問】問題
下の図のような正十角形がある。
全体の面積が \(1\) のとき、斜線部の面積を求めよ。
【日本数学オリンピック(JMO)予選2021第2問】考察
【考察①】まず考えるのが三角形の等積変形
このような面積を求める問題で必ず登場するのが、「三角形の等積変形」です。
【三角形の等積変形】
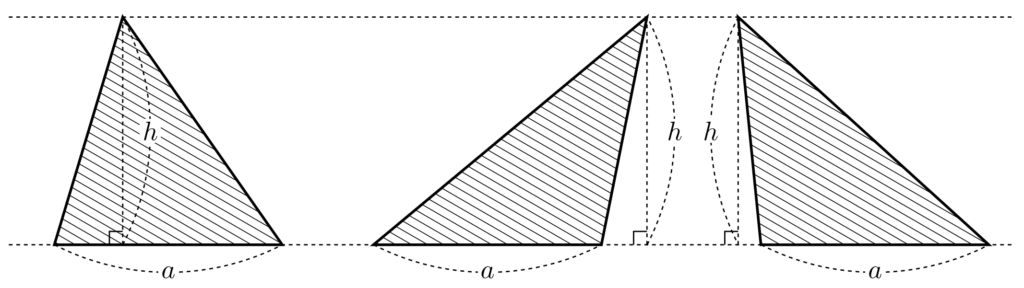
これら3つの三角形の面積は、どれも
\[(底辺) \times (高さ) \div 2 = \frac{1}{\,2\,}ah\]
で等しい。
底辺と高さを固定すれば、3つ目の頂点を横にスライドできます。
この「三角形の等積変形」を使って、斜線部分を一か所にまとめていく方針でいきましょう。
【考察②】対角線をすべて引いてみる
とりあえず、正十角形の対角線をすべて引いてみましょう。
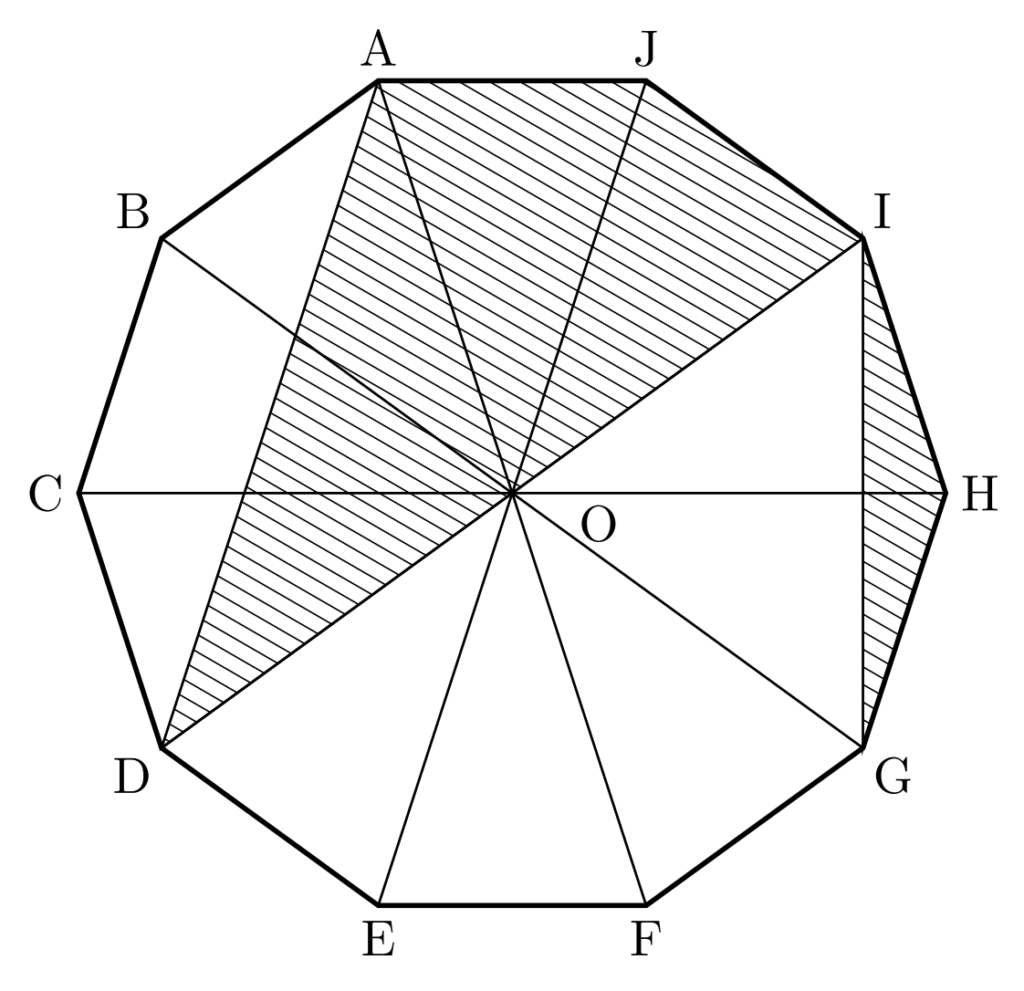
こうすると、例えば
\(対角線 \mathrm{CH} /\!/ 辺 \mathrm{AJ}\)
\(対角線 \mathrm{CH} /\!/ 辺 \mathrm{EF}\)
であることが見えてきます。回転すれば
\(対角線 \mathrm{AF} /\!/ 辺 \mathrm{CD}\)
\(対角線 \mathrm{AF} /\!/ 辺 \mathrm{IH}\)
など、すべての対角線は、それぞれ2つの辺と平行になっているようです。
【考察③】平行線が見つかれば、三角形の等積変形
平行線が見つかれば、三角形の等積変形を使えます。
上の図から、等積変形できそうな三角形は、「\(\triangle\mathrm{ADO}\)」がパッと見つかります。
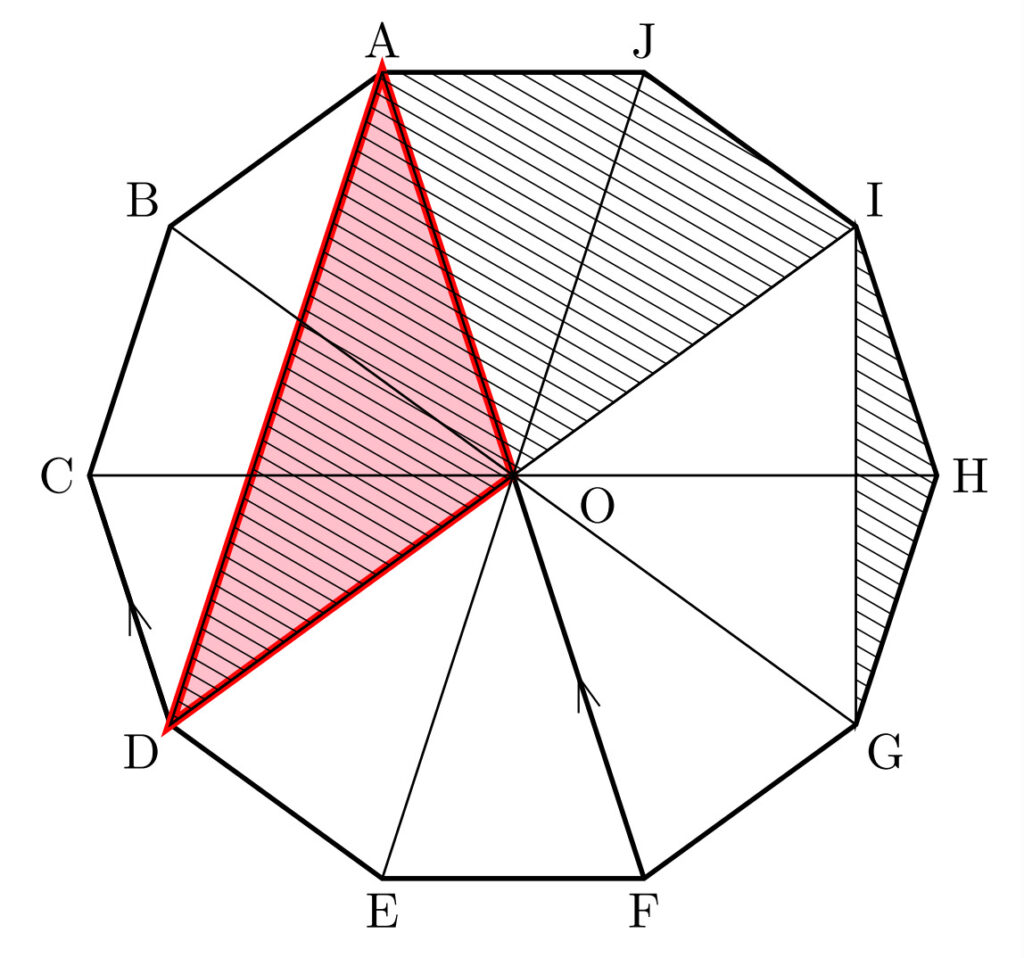
頂点Dを頂点Cに移動すると…
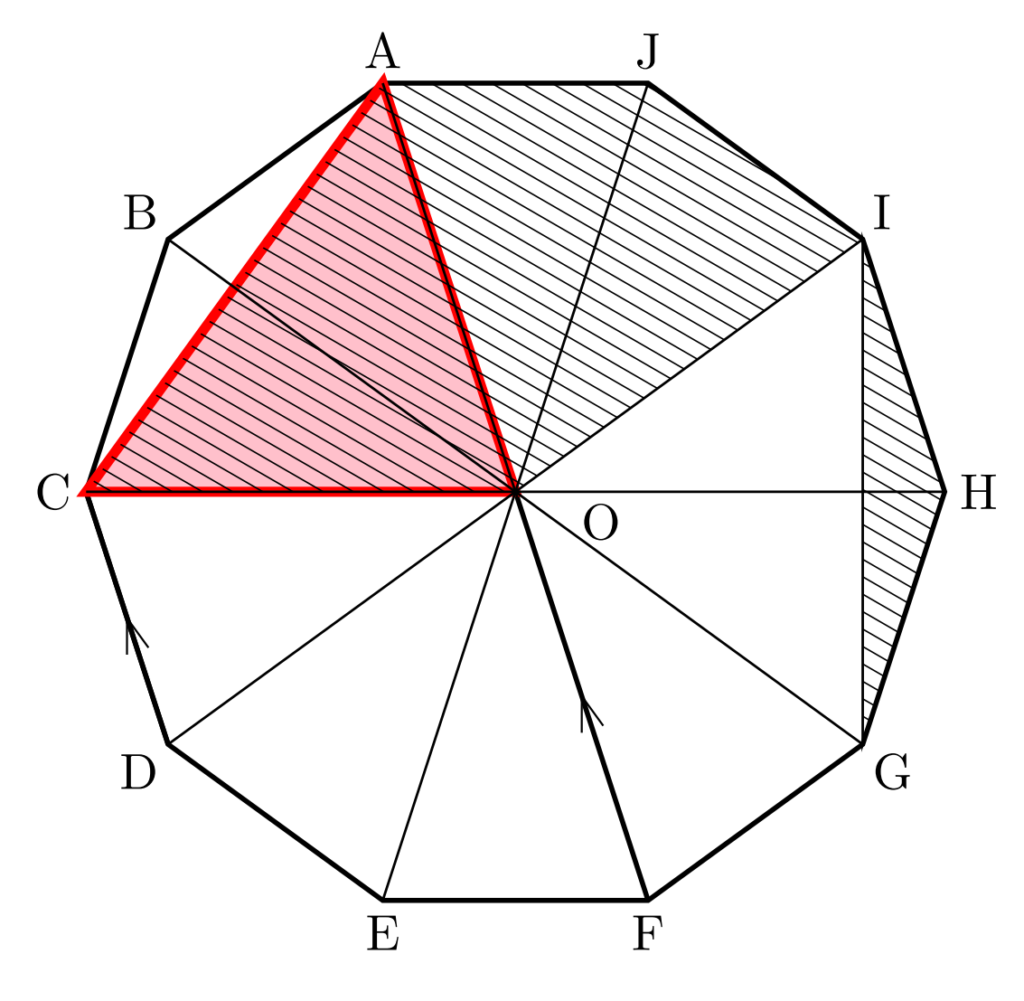
斜線部分の図形は、このように変形できます。
【考察④】小さな三角形を移動する
三角形の等積変形を行ったところ、左上に小さな隙間ができてしまいました。
ここでよく見ると、右側に同じ形の三角形が落ちているではありませんか!
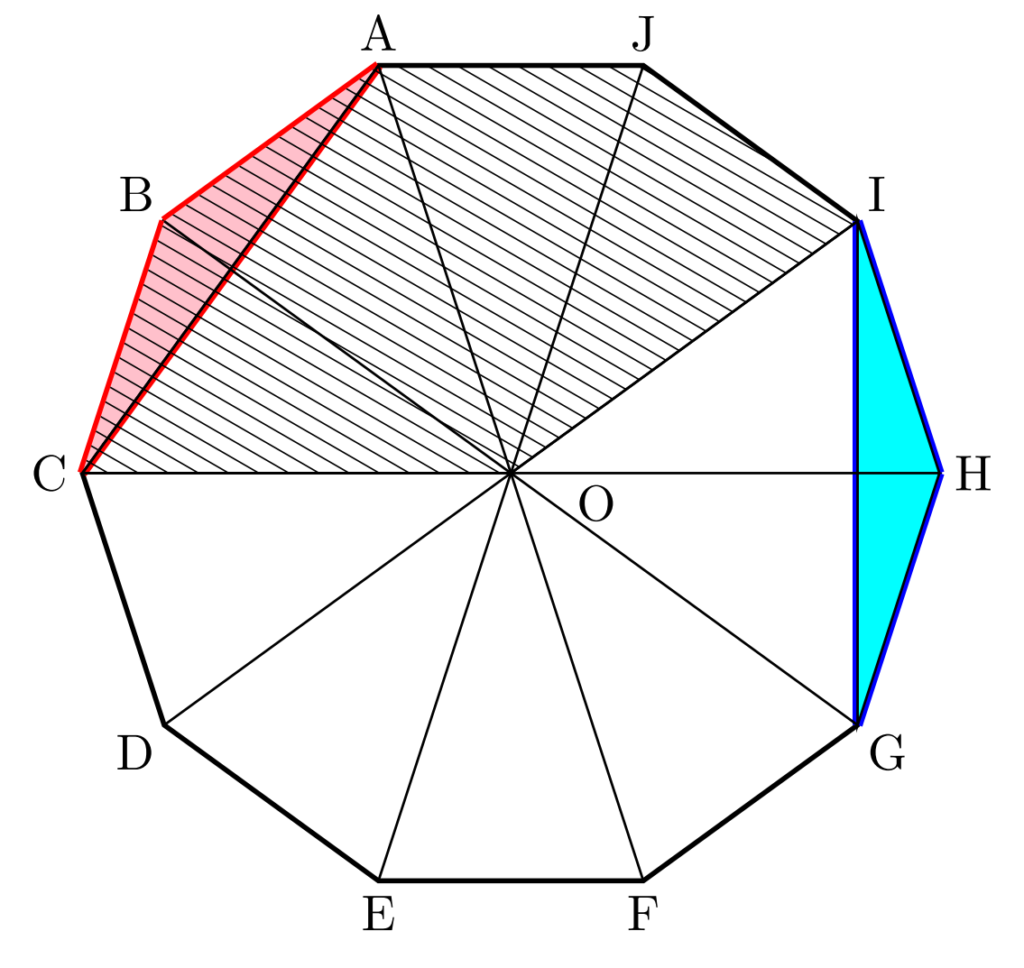
\(\triangle \mathrm{IGH}\) を、\(\triangle \mathrm{ABC}\) の部分へ移動してやれば、斜線部分はすべて正十角形の左上に集まりました。
【考察⑤】面積を求める
さて、いよいよ面積を求めていきます。
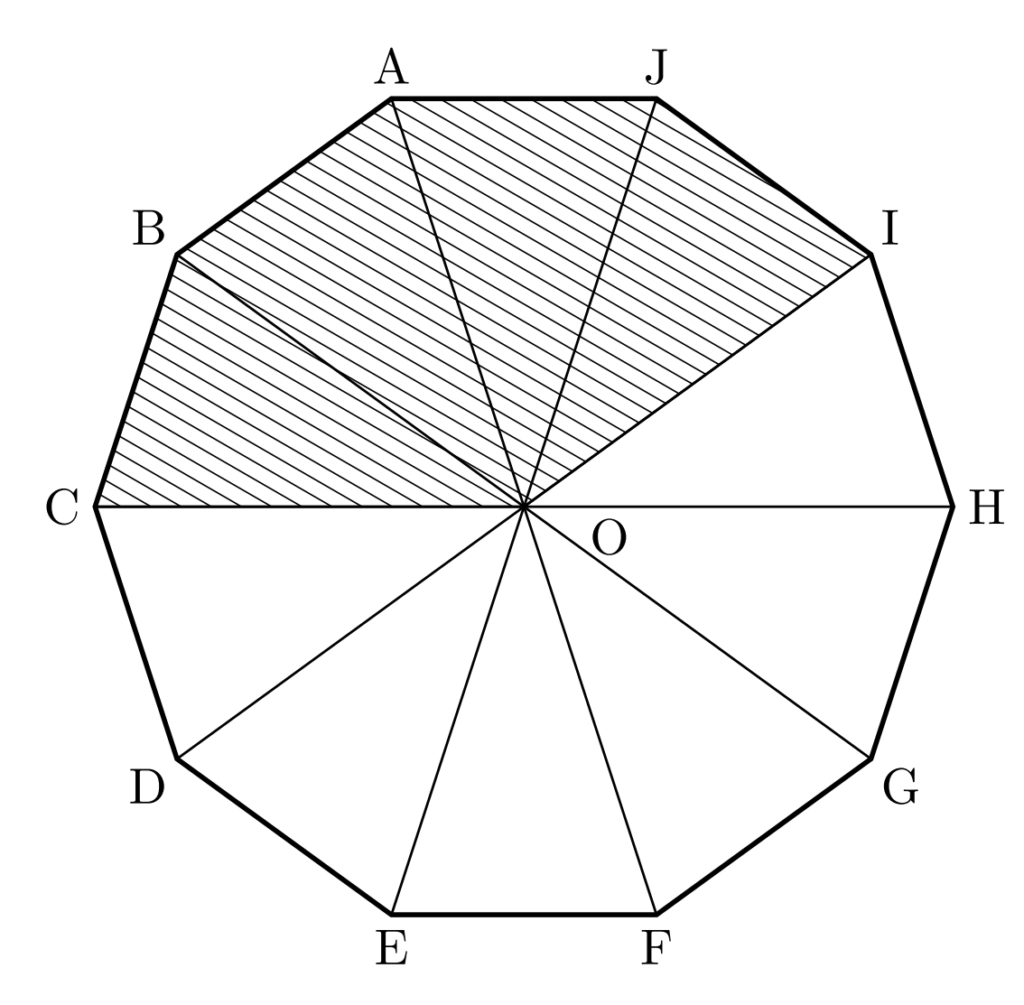
正十角形の面積は \(1\) で、5本の対角線によって10等分されています。
つまり、三角形1つの面積は \(\displaystyle \frac{1}{10}\) です。
斜線部分はこの三角形4つ分なので、これで面積を求めることができそうですね。
【日本数学オリンピック(JMO)予選2021第2問】解答
三角形の各頂点を次のように \(\mathrm{A, B, \cdots, J}\) とし、対角線の交点を \(\mathrm{O}\) とする。

このとき、点 \(\mathrm{O}\) を中心として、頂点 \(\mathrm{A, B, \cdots, J}\) を通る円を描くことができ、各頂点はその円周を10等分している。
円周角の定理から、
\[\angle\mathrm{FAD} = \frac{1}{2} \times \frac{2}{10} \times 360^\circ = 36^\circ\]
\[\angle\mathrm{CDA} = \frac{1}{2} \times \frac{2}{10} \times 360^\circ = 36^\circ\]
であるので、錯角が等しいので
\[\mathrm{AF} /\!/ \mathrm{CD}\]
となる。よって、
\[\triangle\mathrm{ADO} = \triangle\mathrm{ACO}\]
であり、
\[\triangle\mathrm{ABC} = \triangle\mathrm{GHI}\]
であるから、斜線部分の面積は六角形 \(\mathrm{ABCOIJ}\) と等しい。

また、正十角形は合同な三角形10個に分割されており、六角形 \(\mathrm{ABCOIJ}\) はその三角形4個分と等しいので、
\[六角形 \mathrm{ABCOIJ} = 1 \times \frac{4}{10} = \frac{2}{5}\]
【日本数学オリンピック(JMO)予選2021第2問】まとめ
いかがだったでしょうか。
難しい知識は必要なく、必要な知識は三角形の等積変形だけ。
ひらめきさえあれば中学生でも解けてしまうような問題でした。
最後まで読んでいただき、ありがとうございました!
ご意見やご感想、質問などあれば、コメント欄にお願いします👇


コメント