こんにちは。福田泰裕です。
集団のデータの散らばり具合を数値化した「標準偏差」という指標があります。
この標準偏差を見ることで、どれほど散らばりがあるのかが分かります。
標準偏差は、分散の正の平方根です。
標準偏差の意味については、こちらの記事をご覧ください👇
この記事では、EXCELで標準偏差を求めることができるSTDEV.P関数の使い方について解説していきます。
最後まで読んでいただけると嬉しいです。
目次
STDEV.P関数の使い方
STDEV.P関数は、指定された範囲のデータから標準偏差をもとめる関数です。

引数はただ1つで、標準偏差を求めたいデータを選択するだけです。
STDEV.P関数を使い、標準偏差を求める
それではSTDEV.P関数を使い、標準偏差を求めてみましょう。

セルN2に、
=STDEV.P(C2:L2)
と入力します👇

Enterを押すと…👇

とても簡単に標準偏差を求めることができました!
STDEV.P関数を実際にどう使うのか
標準偏差を求めることのできるSTDEV.P関数ですが、どのように使えば良いでしょうか。
標準偏差はデータの散らばり具合を表した指標です。
同じくデータの散らばり具合を表す『分散』とは違い、標準偏差は散らばり具合がより具体的に分かります。
VAR.P関数の実用例①:生徒の得点の分布を予想できる
多くの生徒が受験するテストや模試などは、平均点の周りに多くの人が集まり、平均点から遠くなるほど人数が減っていく結果になります。
しかし平均点だけしか見ない場合、どの程度散らばっているのか分かりません👇
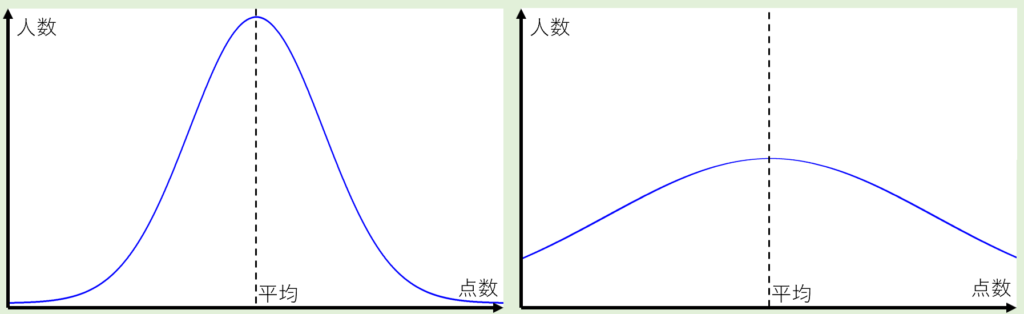
しかし、標準偏差には次のような特徴があります。
平均点を \(\bar{x}\) 、標準偏差を \(s\) とすると、
$$\bar{x} \pm s$$
の範囲に、全体の約 \(68%\) が入っている。
グラフにすると、次のようになります👇
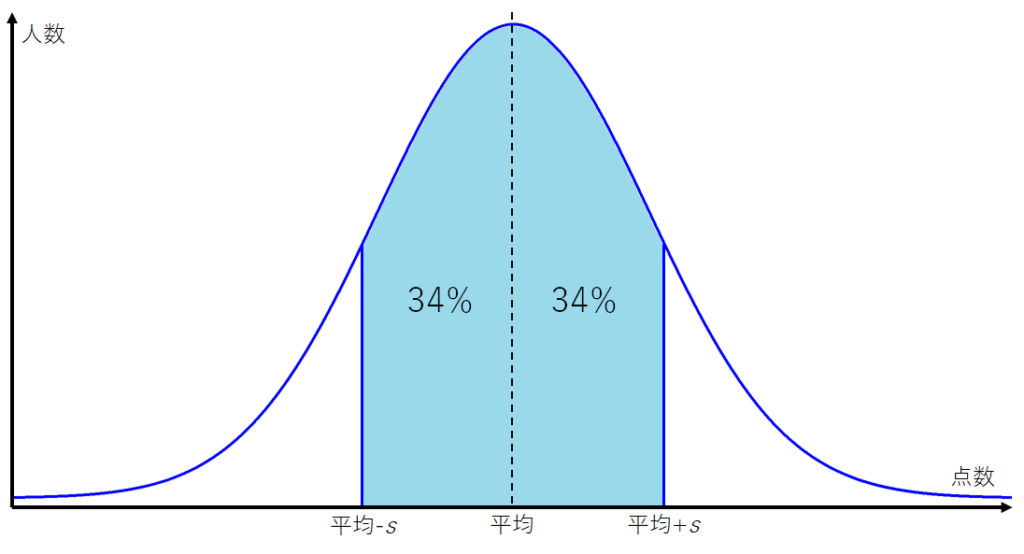
つまり、100人の生徒が受験したテストで平均点が \(60\) 点、標準偏差が \(15.00\)だとすると…👇
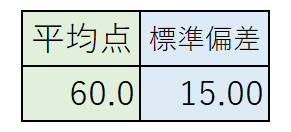
\(60 \pm 15\) 、つまり、\(35~75\) 点の範囲におよそ68人の生徒がいるということです。
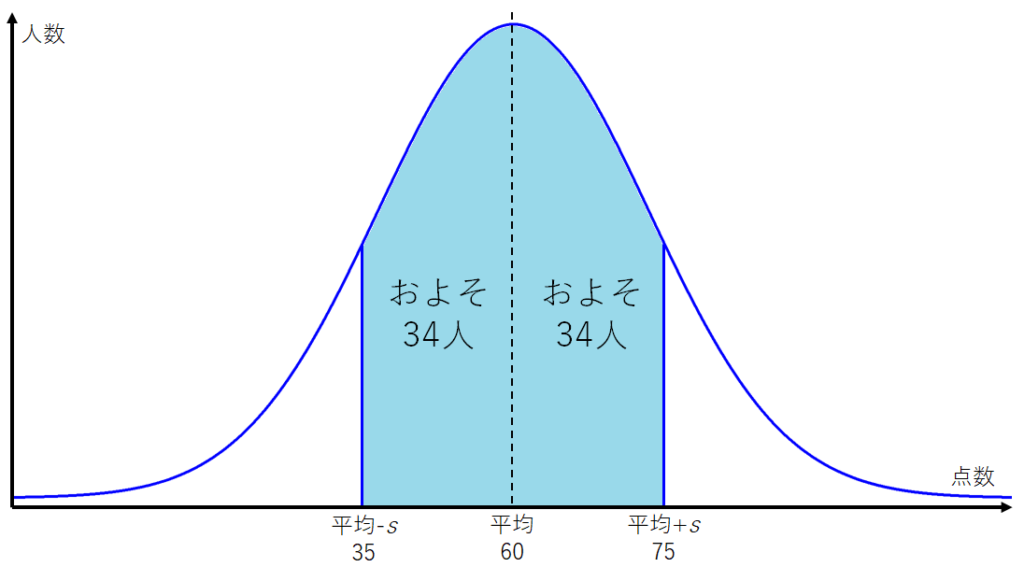
同じ平均点のテストでも、標準偏差が小さいと平均点の近くに多くの人が集まっており、標準偏差が小さいと全体に散らばっているということです。
このように、標準偏差を見ることで全体の得点状況を大雑把に予想できます。
VAR.P関数の実用例②:生徒の偏差値を計算できる
そして、標準偏差を求める最大のメリットは偏差値を計算できることです。
偏差値についての説明は、こちらの記事をご覧ください👇
偏差値は、次の式で求められます。
平均点 \(\bar{x}\)、標準偏差 \(s\) のテストで点数が \(x_i\) だったとき、偏差値は
$$\frac{x_i-\bar{x}}{s} \times 10 + 50$$
この通りにEXCELで数式をつくれば、生徒1人ずつの偏差値を計算することができます。
求め方については、後日記事にまとめるのでお待ちください。
まとめ:標準偏差でテストを分析しよう
いかがでしたでしょうか。
標準偏差はデータの散らばり具合を数値化したものですが、『分散』よりもより具体的なことが多く分かります。
テストを実施した後は平均点だけでなく、標準偏差も求めてみるとよいでしょう。
この記事で紹介したように、全体の得点状況を大雑把に把握できるはずです。
最後まで読んでいただき、ありがとうございました。
質問やご意見、ご感想などがあればコメント欄にお願いします👇



コメント