こんにちは。福田泰裕です。
集団のデータの分布を知るために、四分位数がとても有効です。
EXCELには四分位数を計算するQURTILE関数が用意されています。
しかし、このQURTILE関数を使って四分位数を求めると、手計算で求めた値と違う結果になってしまうことがあります。
この記事では、その理由について解説していきます。
最後まで読んでいただけると嬉しいです。
目次
QURTILE関数と手計算で四分位数を求める

結果が違うって、どういうこと?
という方のために、まずは実際に四分位数を求めてみましょう。
QURTILE関数&手計算での四分位数の求め方
まず、QURTILE関数の使い方はこちらの記事をご覧ください👇
四分位数の計算方法は、こちらの記事をご覧ください👇
10人のデータで四分位数を計算してみる
それでは、実際に求めていきましょう。

上のようなデータを用意しました。
このデータから四分位数を計算していきます。
手計算で四分位数を求める
まず、手計算で四分位数を求めてみましょう。
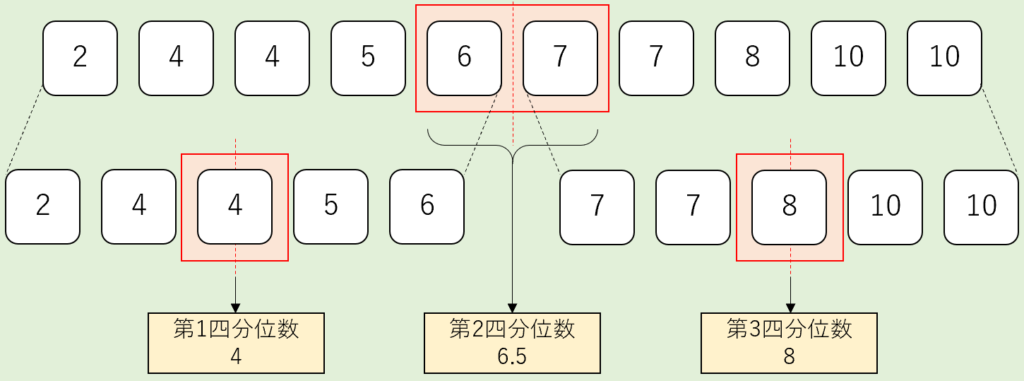
このように、
- 第1四分位数…4
- 第2四分位数…6.5
- 第3四分位数…8
という結果になりました。
QURTILE関数で四分位数を求める
次は、EXCELのQURTILE関数を使って求めてみましょう。

このように、
- 第1四分位数…4.25
- 第2四分位数…6.5
- 第3四分位数…7.75
という結果になりました。
QURTILE関数は、四分位数の求め方が違う
実は、QURTILE関数は四分位数の求め方が手計算の場合と異なります。
手計算で集団を4分割して求めた四分位数を「ヒンジ」といいます。
このヒンジは、手計算でも簡単に求めることのできる簡易的な定義なのです。
それに対して、QURTILE関数のやり方で求めた四分位数を「パーセンタイル」といいます。
このパーセントタイルの四分位数が、一般的な四分位数の定義となります。
四分位数「ヒンジ」では2つのデータの平均を使う
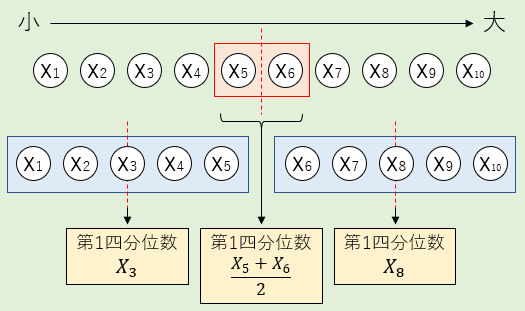
ヒンジでは、半分に分けて第2四分位数を求め、更に半分に分けて第1四分位数、第3四分位数を求めます。
半分にする際にデータの個数が偶数の場合、その中間点を跨ぐ2つのデータの平均を取ります。
四分位数「パーセンタイル」では厳密に4等分する
一方パーセンタイルでは、データの幅を厳密に4等分して、内分点を求める要領で四分位数を求めていきます。
例えばデータが10個の場合、そのデータの幅は9です。
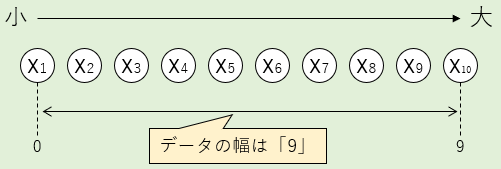
この幅「9」を4等分します。
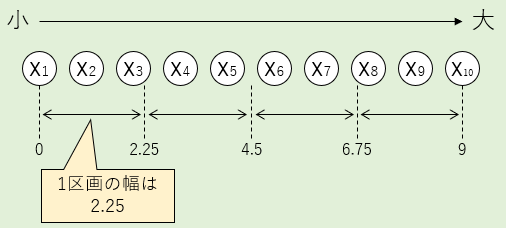
第2四分位数を表すポイントは4.5でちょうど真ん中なので、X5とX6の平均で問題ありません。
しかし、第1四分位数を求めるポイントは2.25となり、X3とX4の間に位置していますが、ややX3に寄っています。
X3とX4の間を拡大すると…👇
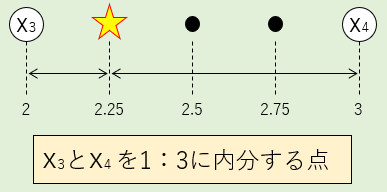
この「2.25」というポイントは、X3とX4を1:3に内分する点なのです。
内分点を求める要領で計算すると…
$$\frac{3 \cdot X_3 + 1 \cdot X_4}{1+3}= \frac{3X_3 + X_4}{4}$$
となります。
これがパーセンタイルでの第1四分位数の求め方です。
同様に考えると、第3四分位数は
$$\frac{X_7+3 X_8}{4}$$
となります。
四分位数が違っても良いのか?

定義の仕方によって、値が変わってもいいの!?
と思われるかもしれません。
確かに、数学のテストのときに答えが2種類あると混乱するかもしれません。
しかし実際に統計を取る際には、「四分位数がいくらか」ということよりも「データの分布はどうなっているのか」が目的となります。
定義の仕方が違いますが、ヒンジとパーセンタイルのどちらの方法でも、四分位数の値はそこまで変わりません。
手計算で求めるならヒンジの方が早いですし、コンピュータを使うならより厳密に分割したパーセンタイルを使う…ということでも、特に問題はないのではないでしょうか。
まとめ:四分位数が違っても焦らずに!
いいかがでしたでしょうか。
手計算で求めた四分位数とEXCELで求めた四分位数が違うと、焦ってしまうものです。
しかし、四分位数にはヒンジとパーセンタイルという2つの定義があり、手計算ではヒンジ、EXCELではパーセンタイルを使っていることを知っておけば、いちいち焦ることもなくなります。
EXCELのQURTILE関数はとても便利な関数なので、分布を調べたいときに活用していきましょう!
最後まで読んでいただき、ありがとうございました!
質問やご意見、ご感想などがあればコメント欄にお願いします👇


コメント
[…] ※この資料がわかりやすかったぞ!→教師のEXCEL口座 […]