こんにちは。福田泰裕です。
テストを実施してクラスの点数一覧が出たとき、平均点を他のクラスと比べて一喜一憂していませんか?
全体の点数を見るための代表値として、平均値というのはとても有名で最もよく使われています。
しかし、代表値は平均値だけではありません。
この記事では、四分位数を調べて箱ひげ図で全体を把握する方法についてご紹介します。
最後まで読んでいただけると嬉しいです。
目次
中央値の意味と求め方
全体の分布を知るために、まずは中央値を求めます。
中央値は、全員を点数の高い順に並べたとき、ちょうど真ん中の順位に位置する人の点数のことです。
しかし、そのグループの人数が奇数か偶数かによって、求め方は少し変わってきます。
人数が奇数の場合の中央値の求め方
人数が奇数の場合は、簡単に中央値を求めることができます。
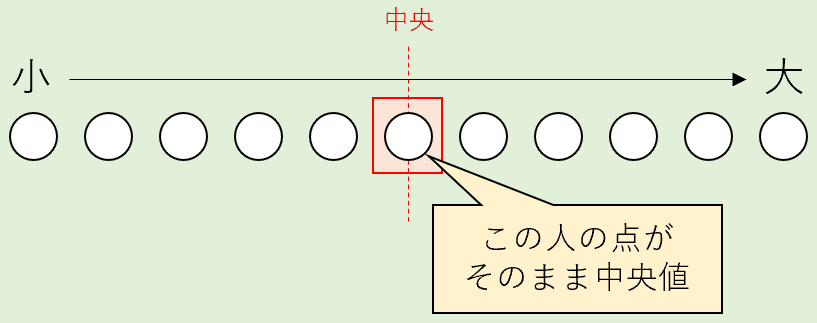
全員を得点順に並べて、ちょうど真ん中の順位に位置する人の点数がそのまま中央値になります。
人数が偶数の場合の中央値の求め方
次に、人数が偶数の場合の中央値の求め方です。
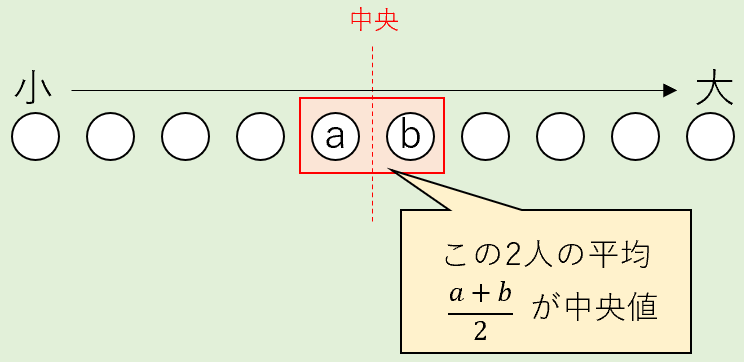
偶数の場合は、半分に割ったときにちょうど真ん中の人がいません。
そのため、その前後の2人の平均を中央値とします。
四分位数の意味と求め方
次に、四分位数を求めていきます。

四分位数って何?
という方も多いと思います。
四分位数などを含めたデータの分析は2012年度から高校1年生で履修する数学Ⅰで学習していましたが、2020年度からは中学2年生の学習内容へ移行されます。
つまり、これからは四分位数は中学で習う常識として扱われるのです!
そのため、これからは知っていないと恥ずかしい世の中になっていきます。
四分位数とはその名の通り、全体を4つに分けた数です。
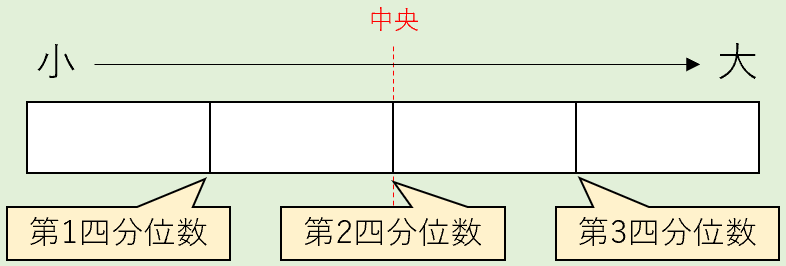
集団を小さい順に並べて4つに分け、
- 1つ目と2つ目の間を「第1四分位数」
- 2つ目と3つ目の間を「第2四分位数」=「中央値」
- 3つ目と4つ目の間を「第3四分位数」
と呼びます。
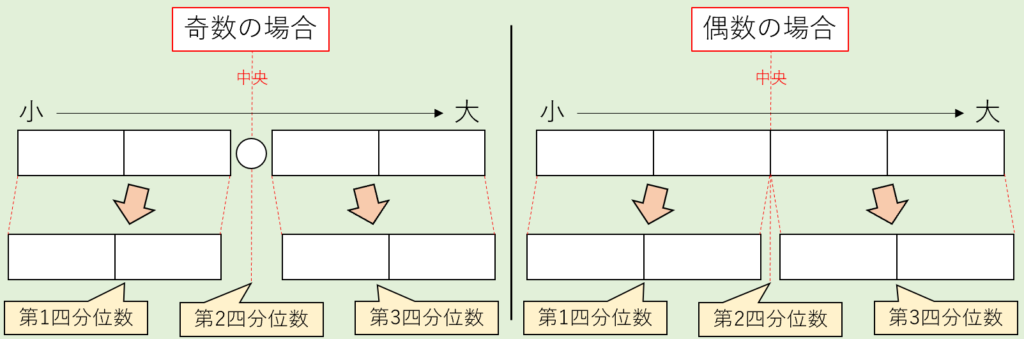
求め方は、まず第2四分位数(=中央値)を求めます。
データの個数が奇数ならば中央のデータを除いて二分し、偶数ならばそのまま二分します。
二分した前後のデータでそれぞれ同じように中央値を求めれば、それが第1四分位数、第3四分位数になります。
まとめ:四分位数を求めて、全体の分布を把握しよう
いかがでしたでしょうか。
集団全体の状況を把握したいとき、平均値だけでは全体の分布を知ることはできません。
最大値、四分位数、最小値、平均点を見ることで、全体の分布を何となくつかむことができます。
この四分位数を知った後は、ぜひ箱ひげ図も知ってほしいと思います。
箱ひげ図は、全体の得点状況を把握するためにとても有効なグラフです。
後日、記事にするのでもうしばらくお待ちください。
最後まで読んでいただき、ありがとうございました!
質問やご意見、ご感想などがあればコメント欄にお願いします👇



コメント