こんにちは。福田泰裕です。
高校の数学Bで数列を学習し、数学Ⅲで数列の極限まで発展します。
そこで出てくるのが「数列の収束」です。
実は、この高校で学習する数列の収束は厳密な定義を隠して何となくのイメージだけで進めているのです。
今回は、数列の収束の定義について解説していきます。
最後まで読んでいただけると嬉しいです。
目次 [hide]
数列の収束の定義

高校の数学Ⅲで学習する数列の収束の定義は、次のようなものです👇
「数列
この「限りなく大きく」や「限りなく近づく」という表現は高校の極限でよく出てきますが、なんとも曖昧な表現です。
どこからが限りなく大きい数と言えるのでしょうか?
どこまで近づけば限りなく近づいたと言えるのでしょうか?
分かりませんよね。
大学で数学を専攻すると、このような曖昧な表現は出てきません。
代わりに、数列の収束の定義が次のように変わります👇
任意の正の数
となるとき、
「数列
「限りなく大きく」や「限りなく近づく」という表現はなくなりました。
しかし、何を言っているのかまったく分からないと思います。
簡単に言うと、どんな正の数
このように、数列の収束には
イプシロン-エヌ論法で数列の収束を証明しよう

とは言っても、上の説明で理解できる人は多分いないでしょう 笑
例題を解きながら解説していきます。
【例題】
数列
高校までは、こんなことは「当たり前」ということで証明しません。

分母が無限に大きくなって、分子は1のまま。
分母の方が圧倒的に大きいから、極限値は 0 です!
と、この説明で十分です。
しかし、大学の数学ではこのような曖昧な表現は許されません。
エプシロン-エヌ論法で証明してみましょう。
具体例で考えてみよう
イプシロン-エヌ論法とは、 どんな正の数
今回の極限値は
どんな正の数
となるような
まず、
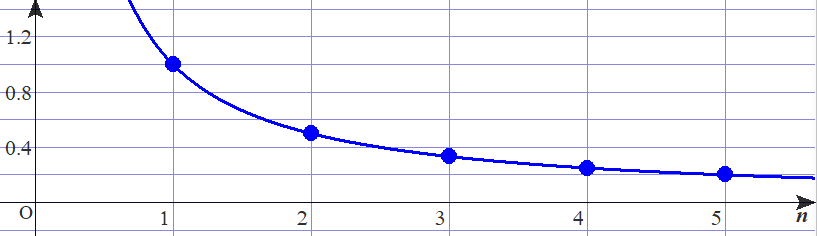
このように、
それでは、何番より先が 0.1 未満になるでしょうか?
そう、だんだん小さくなっていくので、
つまり、
が成り立ちます。
それでは、
今度は
つまり、
が成り立ちます。
それでは、
今度は
つまり、
が成り立ちます。

逆数にすれば良いの?
と考えるかもしれませんが、そんな単純でもないのです。
数列の番号は自然数なので、逆数が通用しない場合もあります。
それでは最後の例として、
今度は
つまり、
が成り立ちます。
このときの
の逆数
の整数部分を
実際に代入する
この調子でいけば、
しかし
そのため、証明は次のように行います。
【証明】
任意の正の数
とする。このとき、
であるから、
が成り立つ。
よって、数列
は?
と思われたかもしれませんが、これで証明は終わりです。
簡単に言えば、
どんな
これで、無限にある
まとめ:イプシロン-エヌ論法は静的なイメージ

いかがでしたでしょうか。
高校での数列の収束というのは、「
高校までの数列の収束とは考え方がまったく異なるので、なかなかイメージしにくいかもしれません。
しかし、厳密な証明方法を知ることで、高校での極限の考えを学ぶ際に役に立つことがあるかもしれませんね。
最後まで読んでいただき、ありがとうございました!
質問やご意見、ご感想などがあればコメント欄にお願いします👇


コメント