こんにちは。福田泰裕です。
集合写真を撮影するとき、「はい、チーズ!」で撮影します。
しかし、必ず目をつぶってしまう人がいますよね。
今回は、集合写真を何枚撮影すれば全員の目が開いた写真が撮影できるのか、確率を計算しながら解説します。
最後まで読んでいただけると嬉しいです。
目次
集合写真で全員の目が開いている確率を求める
それでは、集合写真で全員の目が開いている確率を求めていきましょう。
問題をハッキリさせる
まず、問題をハッキリさせましょう。
人間は、6秒ごとに0.25秒の瞬きをしているといわれています。
また、一般的なカメラのシャッター速度は、明るい所だと \(\displaystyle \frac{1}{125}\) 秒です。
このことから、問題を次のように考えましょう。
人間は、6秒ごとに0.25秒は目をつぶっている。
カメラのシャッター速度は、 \(\displaystyle \frac{1}{125}\) 秒である。
\(n\) 人で集合写真を撮影するとき、全員が目を開けて撮影できる確率を求めよ。
それでは、考えていきましょう!
1人が目を開けて撮影できる確率を考える
まずは集合写真ではなく、1人が目を開けて撮影できる確率を考えてみましょう。
人間の瞬きは6秒ごとに0.25秒です。
つまり、目を開けている時間は6秒あたり
\(6 – 0.25 = 5.75\) (秒)
です。
そこに、 \(\displaystyle \frac{1}{125} = 0.08 \) 秒でシャッターを切ればよいのです。
目を開けた写真を撮影することができる時間は、6秒あたり
\(5.75 = 0.08 = 5.742 \) (秒)
となります。
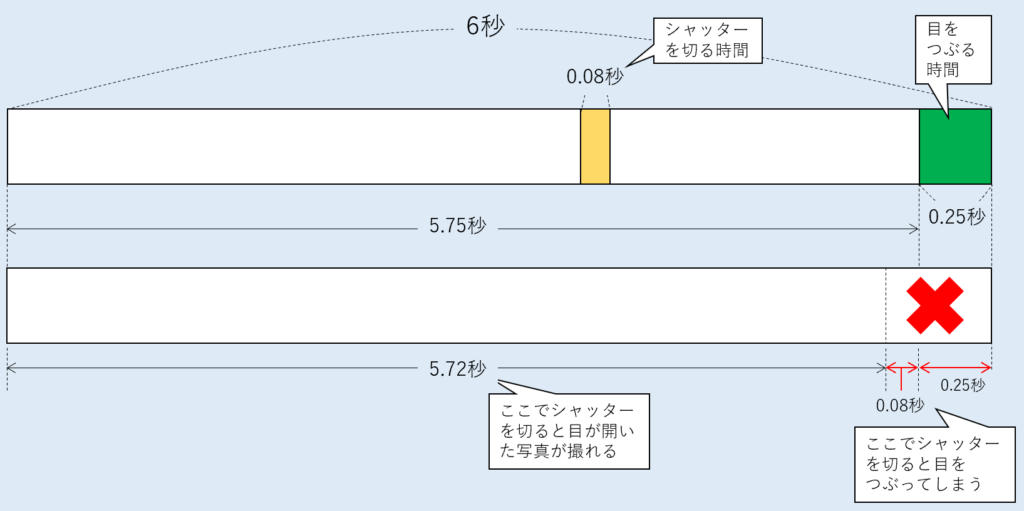
1人が目を開けて撮影できる確率は、 6 秒のうち 5.742 秒なので、
\(\displaystyle \frac{5.742}{6} = \frac{957}{1000} = 95.7 \%\)
となります。
n人全員が目を開けている確率を考える
これを元に、\(n\) 人全員が目を開けている確率を求めましょう。
1人が目を開けて撮影できる確率は
\(0.957\)
なので、\(n\) 人全員が目を開けて撮影できる確率は
\(\displaystyle 0.957^n\)
となります。
これを、EXCELを使って計算してみると…
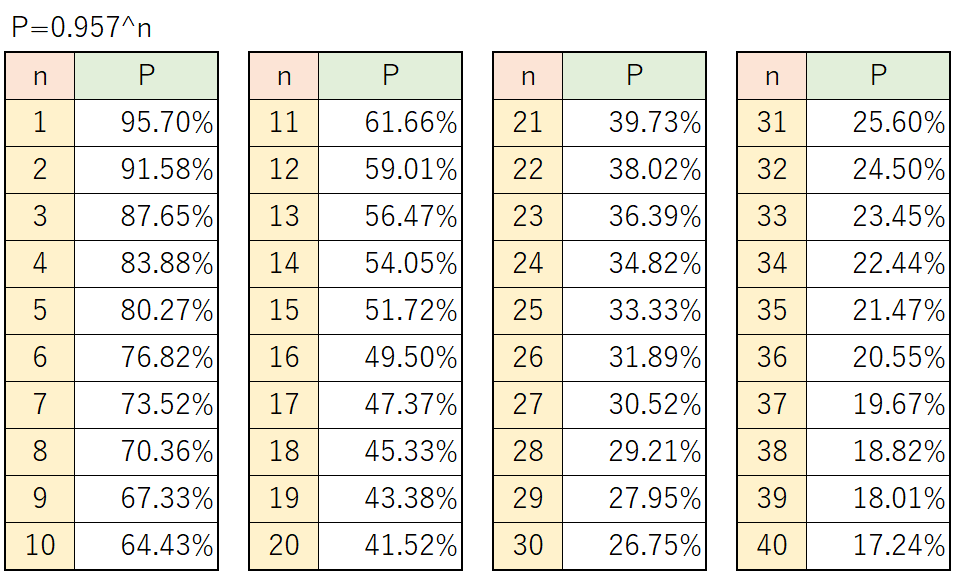
このような結果になりました。
30人クラスの場合、約26%なので4回に1回しか全員の目が開いていないことが分かりますね。
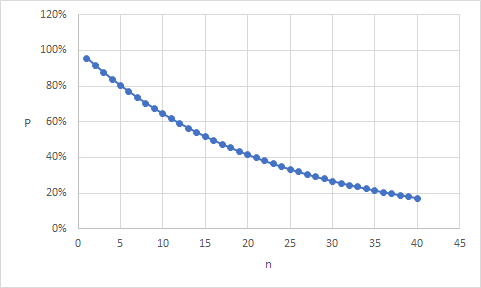
グラフにすると、このようになります👇
確率が1/4だから4枚撮影すれば良い…というわけではない
30人クラスは約26%だから、4枚撮影すれば大丈夫…というわけではありません。
確率が \(\displaystyle \frac{1}{4}\) である事象を4回繰り返して、1回以上起こる確率は、
\(\displaystyle 1 – \left( \frac{3}{4} \right)^4 = 1 – \frac{81}{256} = \frac{175}{256} = 約68.3 \%\)
しかありません。
つまり30人クラスで4枚撮影した場合、全員の目が開いている確率は68.3%しかないのです。
この68.3%の確率を高いと思うか低いと思うかは人それぞれですが、どうせなら確実に目が開いている写真を撮影したいですよね?
全員の目が開いている確率を99%以上にするために必要な撮影枚数を計算する
\(n\) 人の集合写真で全員の目が開いている確率は
\(\displaystyle 0.957^n\)
でした。
つまり、\(n\) 人の集合写真で誰か1人でも目をつぶる確率は
\(\displaystyle 1 – 0.957^n\)
です。
ということは、写真を \(m\) 枚撮影して、写真がすべて失敗する(少なくとも1人は目をつぶっている)確率は、
\(\displaystyle \left( 1 – 0.957^n \right)^m\) ‥‥‥①
となります。
全員の目が開いている写真を1枚以上撮影できる確率を \(99 \% \) 以上にしたいとき、失敗する確率は \(1 \% = \frac{1}{100}\) 未満に抑えなければならないので、
\(\displaystyle \left( 1 – 0.957^n \right)^m < \frac{1}{100}\)
という式を満たす \(m\) を求めることになります。
両辺の常用対数をとると、
\(\displaystyle m \log _{10} \left( 1 – 0.957^n \right) < \log_{10} 10^{-2} = -2 \)
両辺を \(\displaystyle \log _{10} \left( 1 – 0.957^n \right) (<1) \) で割って、
\(\displaystyle m > – \frac{2}{ \log _{10} \left( 1 – 0.957^n \right) } \)
となります。
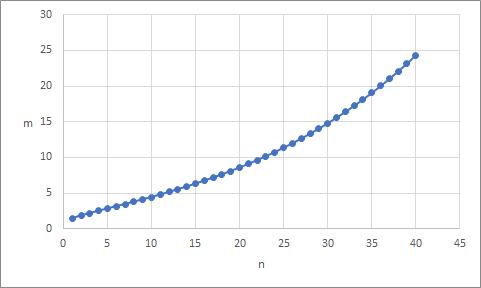
確率が99%以上になるための撮影枚数と人数の関係
それでは、この結果を考察していきます。
EXCELを使って、確率99%となる撮影枚数 \(m\) を計算してみると…
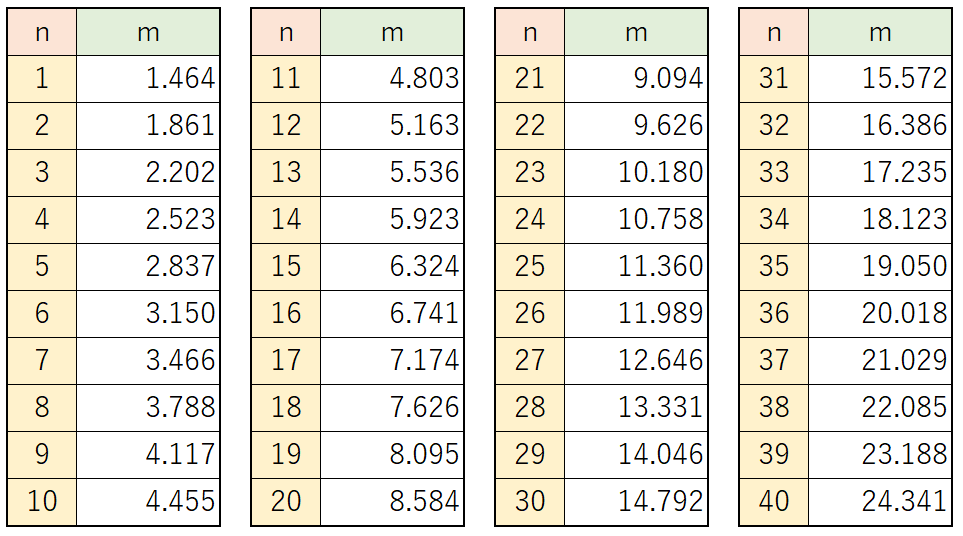
このようになりました。
30人クラスなら、\(m=14.792\) なので 15枚撮影すれば99%の確率で全員の目が開いている写真が撮影できることを意味しています。
35人クラスならば20枚、40人クラスならば25枚撮影すれば良いのです。
グラフは下のようになります。
人数が増えていくと、必要な枚数の増え方も大きくなっていくようですね。
撮影枚数から、全員の目が開いている確率を計算する
でも実際は、1回の撮影で15枚も撮影することはありません。
次は逆に、撮影枚数から確率を計算してみましょう。
①より、\(n\) 人の集合写真を \(m\) 枚撮影したとき、すべての写真で少なくとも1人が目をつぶっている確率は
\(\displaystyle \left( 1 – 0.957^n \right)^m\)
です。
全員の目が開いている写真を1枚以上撮影できる確率を \(p\) とすると、その余事象 \(1-p\) は「すべての写真で少なくとも1人が目をつぶっている確率」となるので、
\(\displaystyle \left( 1 – 0.957^n \right)^m = 1 – p\)
です。
よって、
\(\displaystyle p = 1 – \left( 1 – 0.957^n \right)^m\)
となります。
人数 \(n\) と撮影枚数 \(m\) で、確率がどう変わるか一覧にしました。
(スマホでご覧の方は文字が小さいので、横向きにして見てください!)
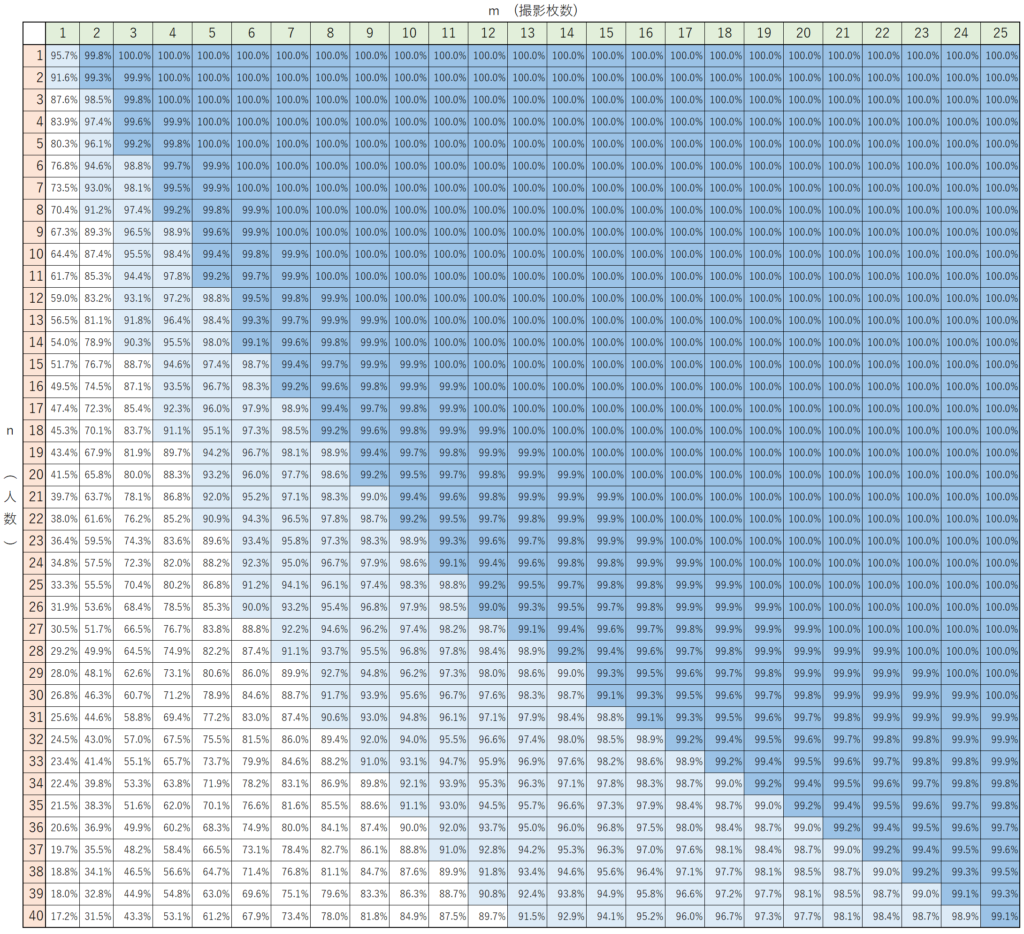
90%以上を薄い青色、99%以上を濃い青色にしています。
3~4枚撮影したくらいでは、全員の目が開いている写真を撮ることは難しそうですね。
2006年イグノーベル賞(数学賞)を受賞した研究である

この集合写真の確率は、2006年のイグノーベル賞(数学賞)を受賞した由緒正しい、人々を笑わせ、そして考えさせてくれる研究です。
オーストラリア国立科学技術研究機構のニック・スヴェンソンとピアース・バーンズの2名が受賞しました。
日常に潜む疑問を、本気で研究した結果ですね。
まとめ:全員の目が開いている写真を撮影できる確率は低い!
いかがでしたでしょうか。
今回の記事をまとめると、次のようになります。
\(n\) 人で集合写真を撮影する。
① 99%以上の確率で全員の目が開いている写真を1枚以上得るためには、
\(\displaystyle – \frac{2}{ \log _{10} \left( 1 – 0.957^n \right) } \) 枚以上撮影する必要がある。
② 写真を \(m\) 枚撮影したとき、全員の目が開いている確率 \(p\) は、
\(\displaystyle p = 1 – \left( 1 – 0.957^n \right)^m\) である。
あなたのクラスの人数を式に当てはめて、写真を何枚撮影すれば良いのか考えてみてください。
一度しかない思い出の場面を全員の目が開いた状態で撮影するためには、計算が必要なのです。
確率って面白いですね!
最後まで読んでいただき、ありがとうございました。
質問やご意見、ご感想などがあればコメント欄にお願いします👇


コメント