こんにちは。福田泰裕です。
席替えとは、学校生活における一大イベントです。
なぜなら、好きなあの子の隣の座席になるかもしれないからです!
実際はなかなかうまくいきませんが、どうしても期待してしまいますよね…?
今回は、席替えで好きな人の隣の座席になる確率を考えていきます。
最後まで読んでいただけると嬉しいです。
目次
席替えで好きな人の隣の座席になる確率を求める
それでは、席替えで好きな人の隣の座席になる確率を求めていきましょう。
クラスの人数と座席を決める
好きな人の隣になる前に、まず好きな人は1人であるということにしましょう。
複数いる人は、一番好きな人に絞ってください。
私をAさん、好きな人をBさんとします。
そしてこの問題は、教室の座席によって結果が変わってきます。
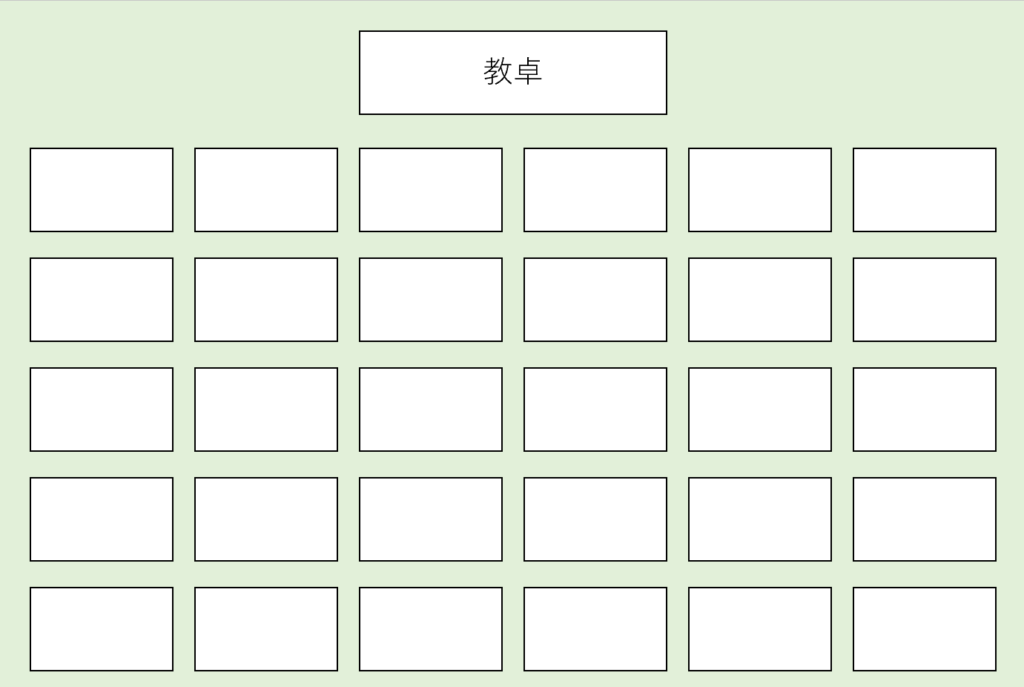
いったん今回は、下のような座席の30人学級で考えてみましょう。
下のような座席の30人学級で席替えを行う。
AさんとBさんが隣の席になる確率を求めよ。
隣の席になる確率を計算する
まず、全事象を考えましょう。
30個の座席から、AさんとBさんの2人が座る2個の座席を選ぶので、\( _{30}\mathrm{P}_2 = 30 \times 29\) 通りです。
次に、2人が隣りの座席になる場合の数を考えます。
座席表から、2人が隣の座席になるパターンは…👇
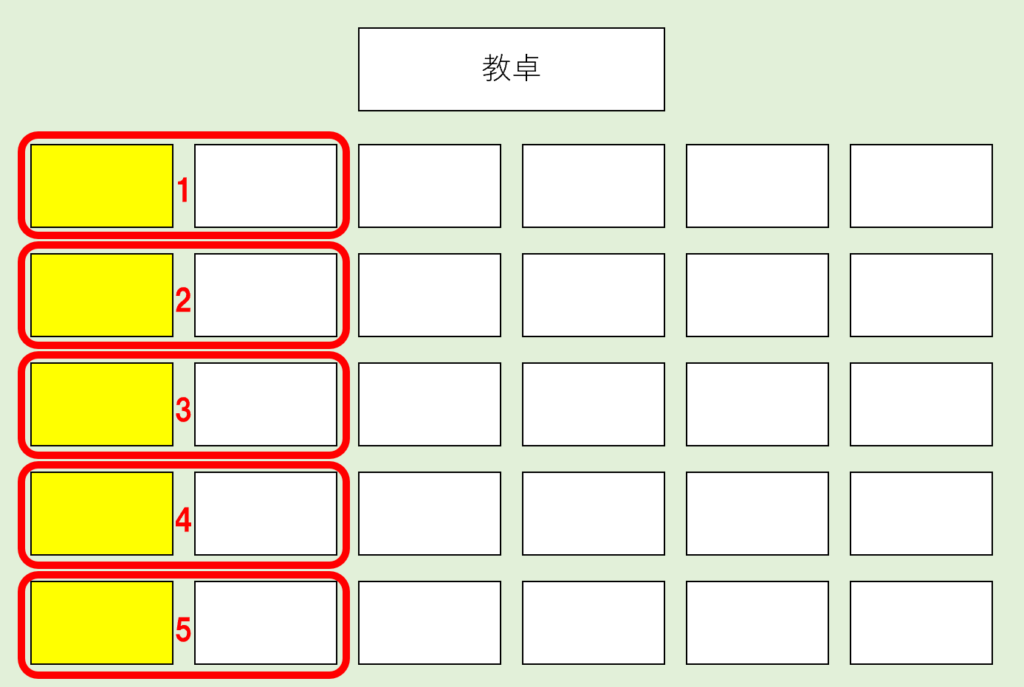
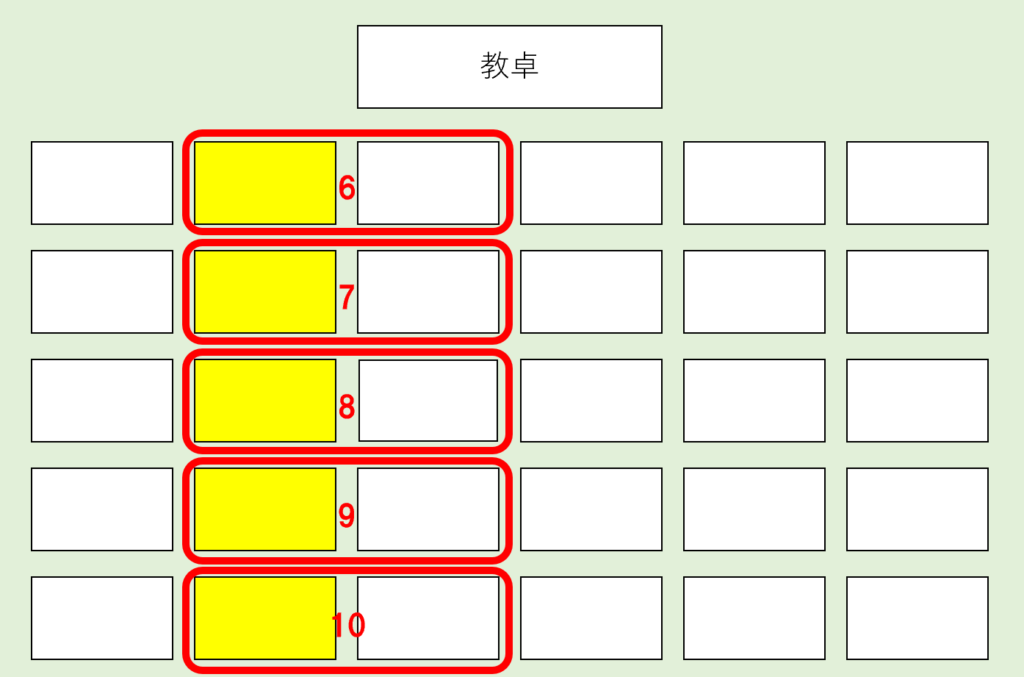
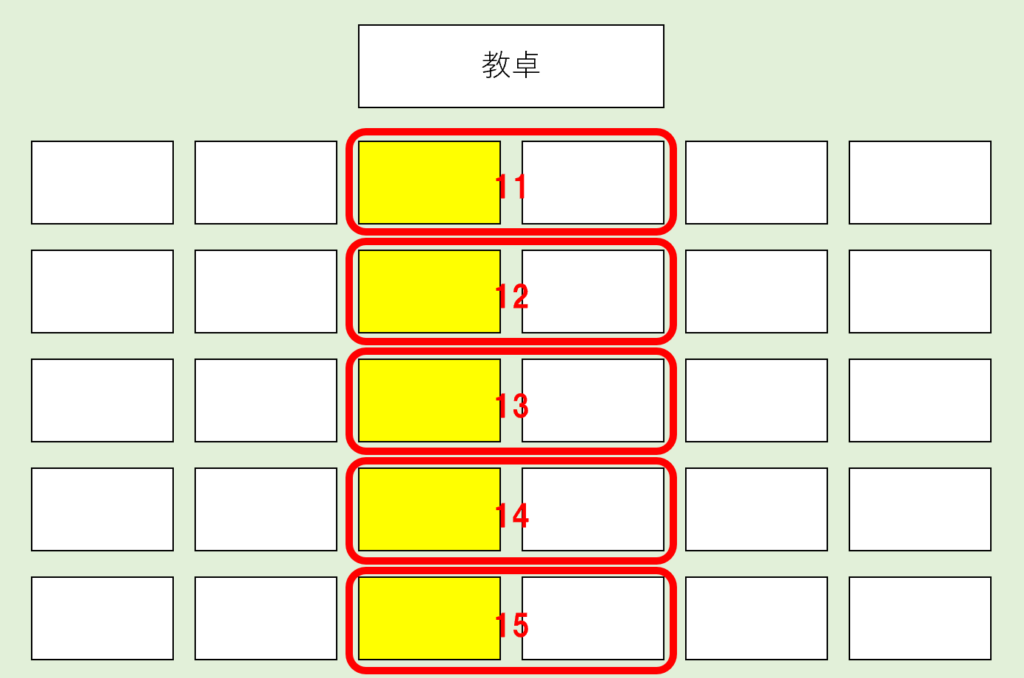
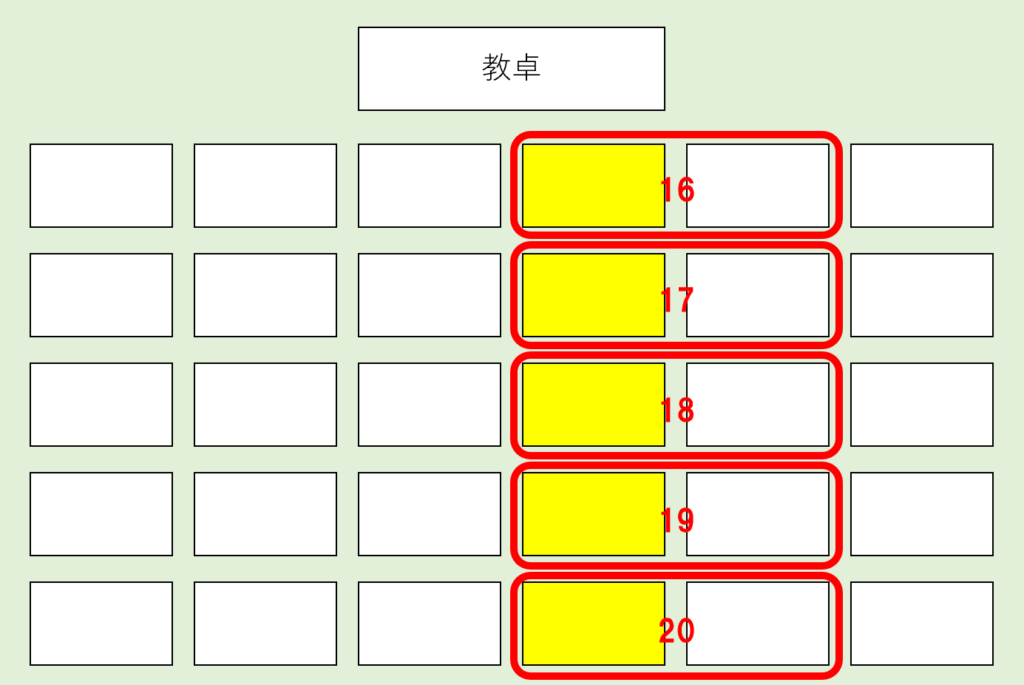
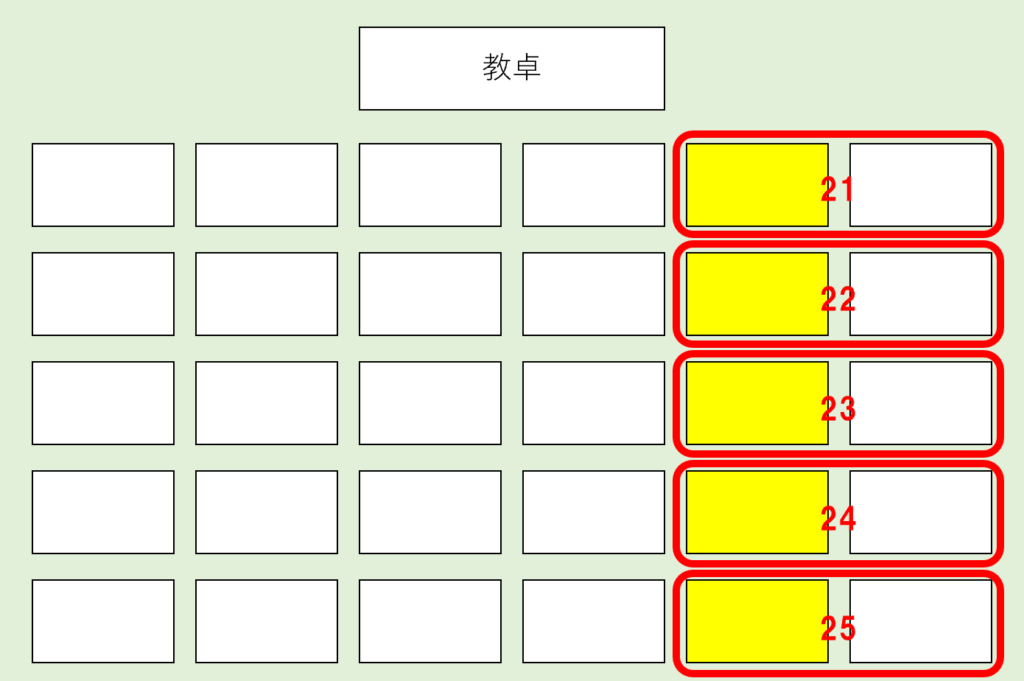
この25通りあります。
さらに、この座席それぞれに「Aさん、Bさん」で座るか、「Bさん、Aさん」で座るかの2通りがあります。
よって、2人が隣の座席になる座り方の場合の数は、\( 25 \times 2\) 通りです。
以上から、求める確率は$$\frac{25 \times 2}{30 \times 29} = \frac{5}{87} = 0.05747‥‥‥=約6\%$$となります。
6%‥‥‥
好きなあの子の隣の座席になるのは難しそうですね‥‥‥。
少しいびつな座席配置で計算してみる
上の例では、6×5=30人の座席で計算しましたが、実際はこんなにスッキリしていない座席もあります。
例えば同じ30人学級で、座席が下のような場合を考えてみましょう。
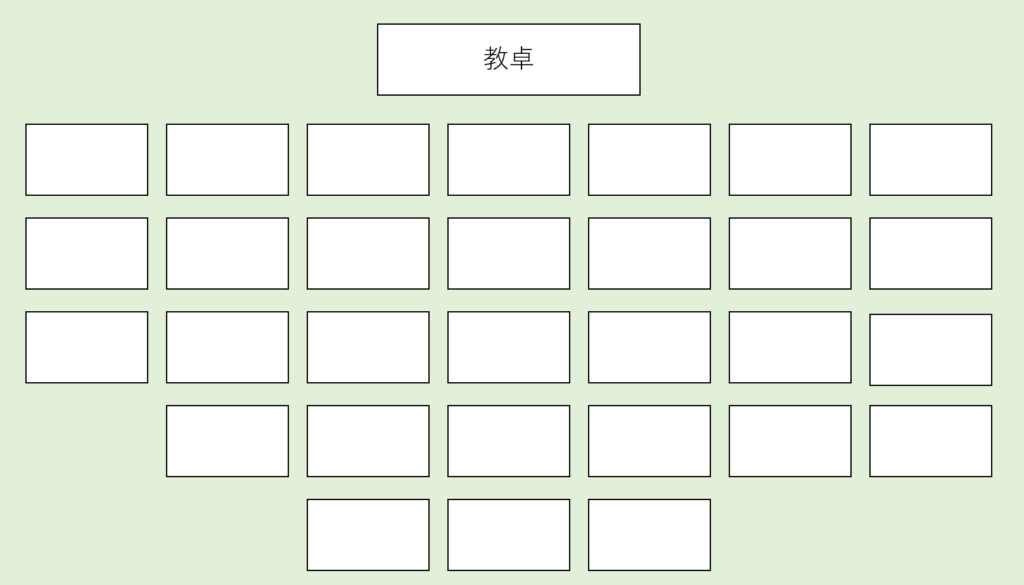
少しいびつな座席になりました。
直感的に、好きな人と隣になれる確率はどうなると思いますか?
A…上がる!
B…同じ!
C…下がる!
予想できましたか?
それでは計算していきましょう。
まず全事象は先ほどと同じく、30個の座席から2個の座席へ座るので、\(30 \times 29\) 通りです。
次に、隣の座席になる座り方の場合の数を数えてみましょう。
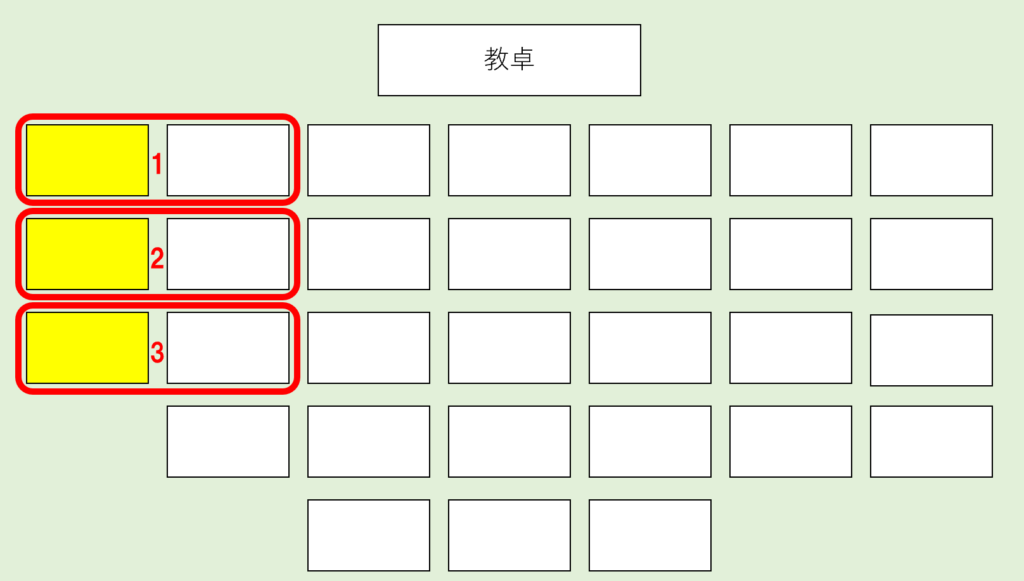
あれ、25通りで先ほどと同じですね。
同じように座り方は「Aさん、Bさん」、「Bさん、Aさん」の2通りずつあるので、\(25 \times 2\) 通りです。
よって、確率は$$\frac{25 \times 2}{30 \times 29} = \frac{5}{87} = 0.05747‥‥‥=約6\%$$ です。
なんと、結果はB…同じでした。
ちょっと意外じゃないですか?
隣の座席になる座り方の「良い数え方」を考える
なんとなく計算のパターンが見えてきました。
隣の座席になるパターンを数えれば良いのですね。
しかし、座席が増えると結構面倒くさいです。
もっと良い方法は無いでしょうか…?
先ほどの2つの例を見てみましょう。
隣の席になる座り方を数えるとき、左側の座席を黄色にしています。
つまり、この黄色の座席には左隣に座席があるということを意味しています。
1つ目の例題で、黄色の座席を集めてみると…👇
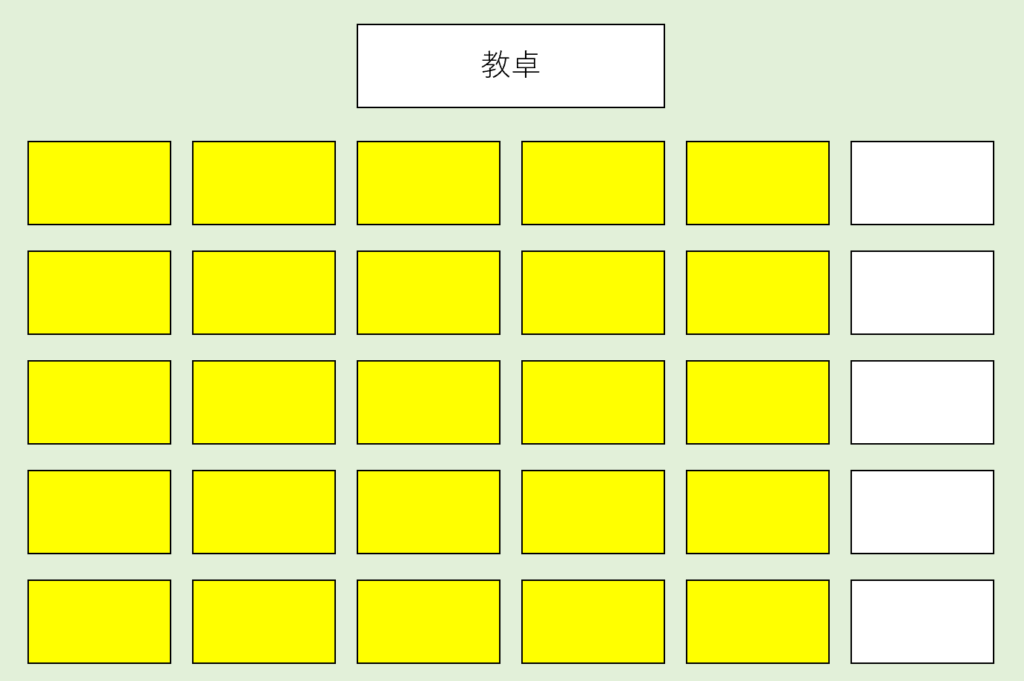
このようになります。(黄色の座席は25個。)
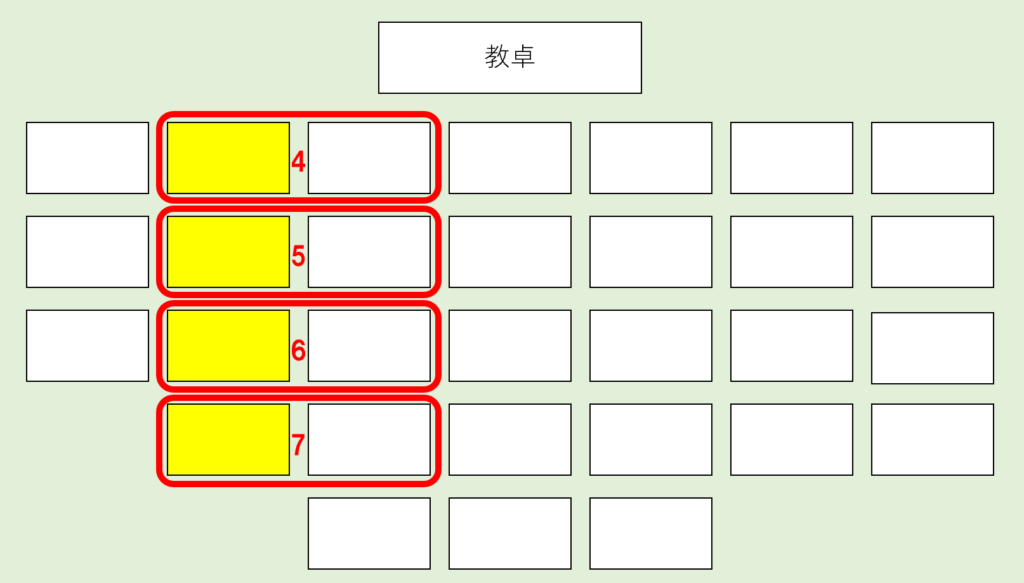
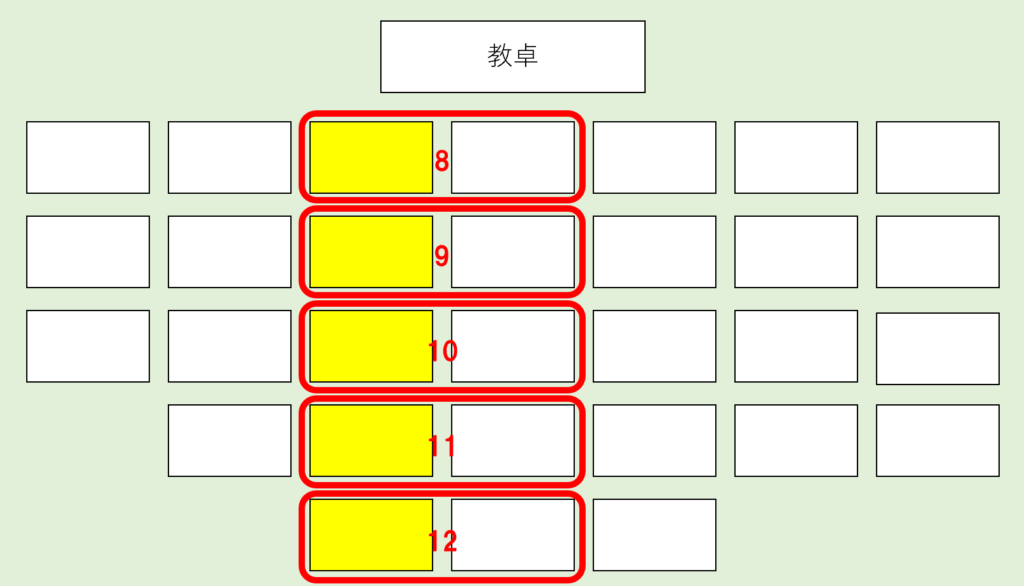
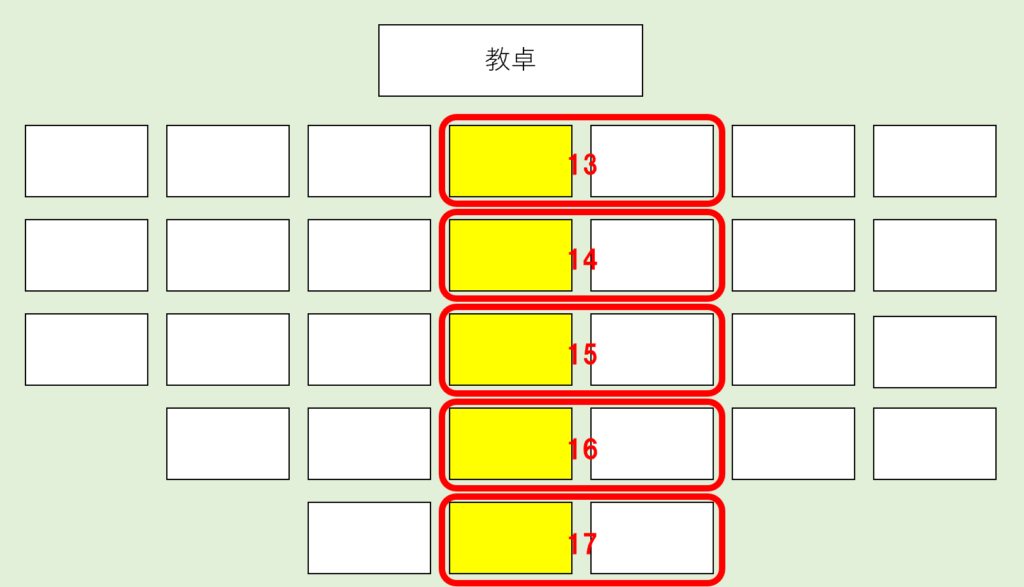
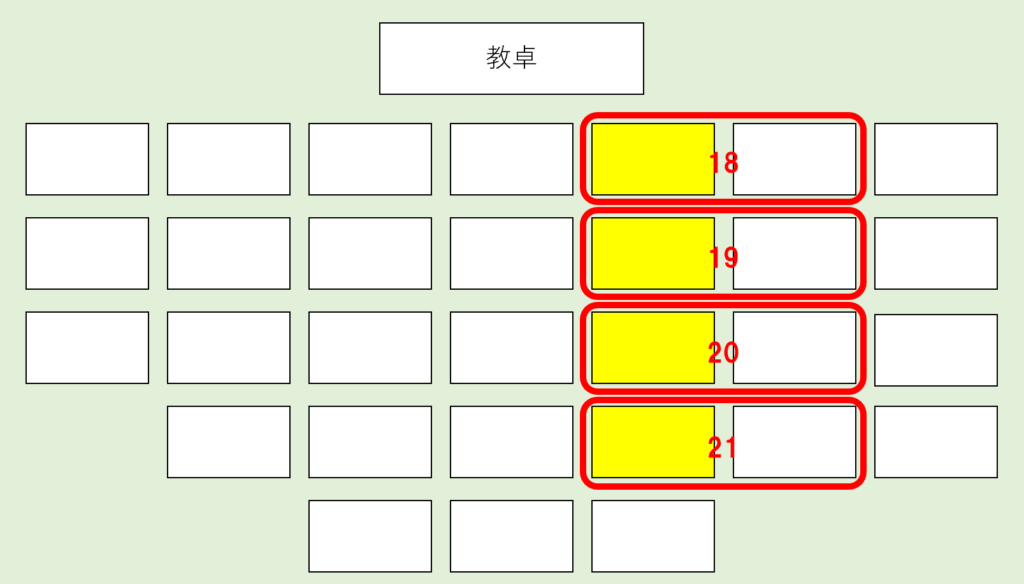
次に2つ目の例題の黄色の座席を集めてみると…👇
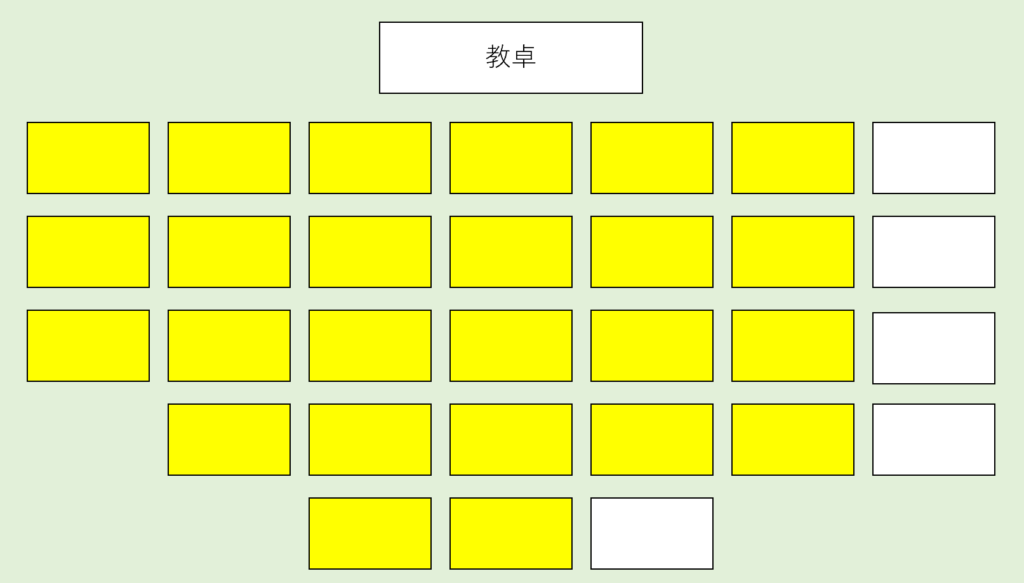
こうなります。(黄色の座席は25個。)
2つの図を見て、黄色になっていない、白い座席の特徴は何でしょうか?
…
そうです!
白い座席には、右隣がありません!
つまり、
「隣の席になる座り方の場合の数」=「すべての座席数」-「右隣がない座席の数」
と言えるのです!
これさえ知っていれば、どんな複雑な座席配置でも簡単に計算できます!
複雑な座席配置でも簡単に数えられる
上のように、
「隣の席になる座り方の場合の数」=「すべての座席数」-「右隣がない座席の数」
という事実を使って、複雑な座席配置で隣の席になる確率を考えてみましょう。
このクラスに一体何があったのか分かりませんが、次のような場合を考えてみます👇
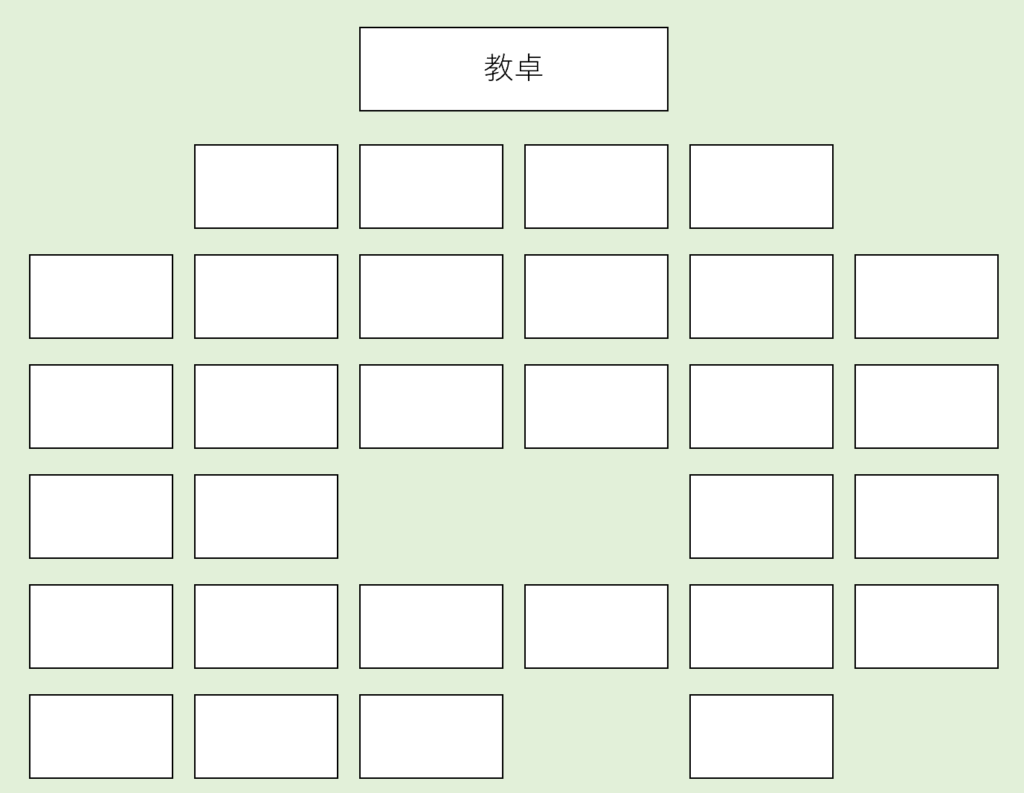
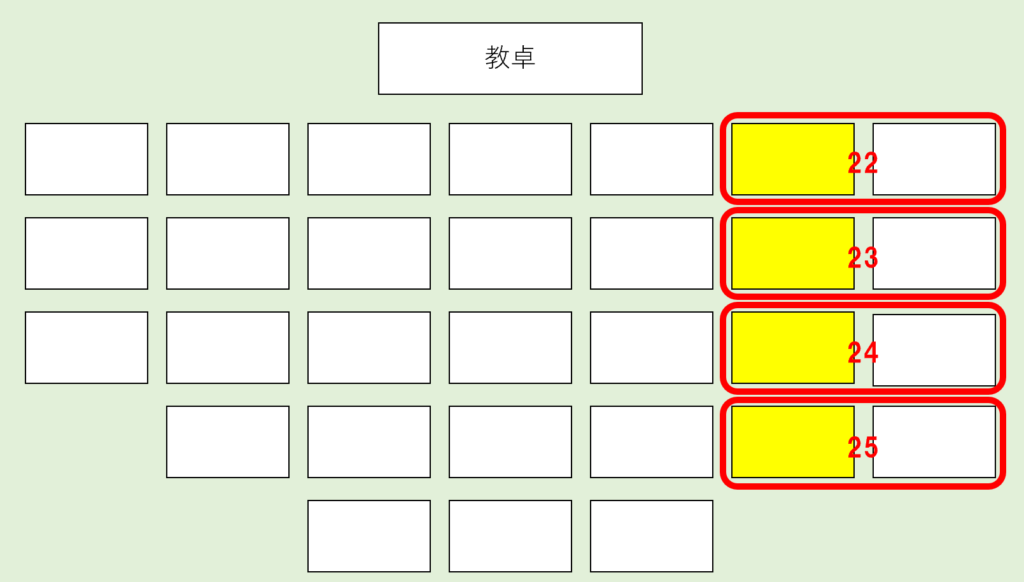
座席数は30個なので、2人の座り方は \(30 \times 29\) 通り。
そして、隣の座席になる座り方の場合の数を数えます。
大丈夫ですよね…?
すべての座席数から、右隣がない座席の数を引けば良いのですね!
右隣がない座席は…👇
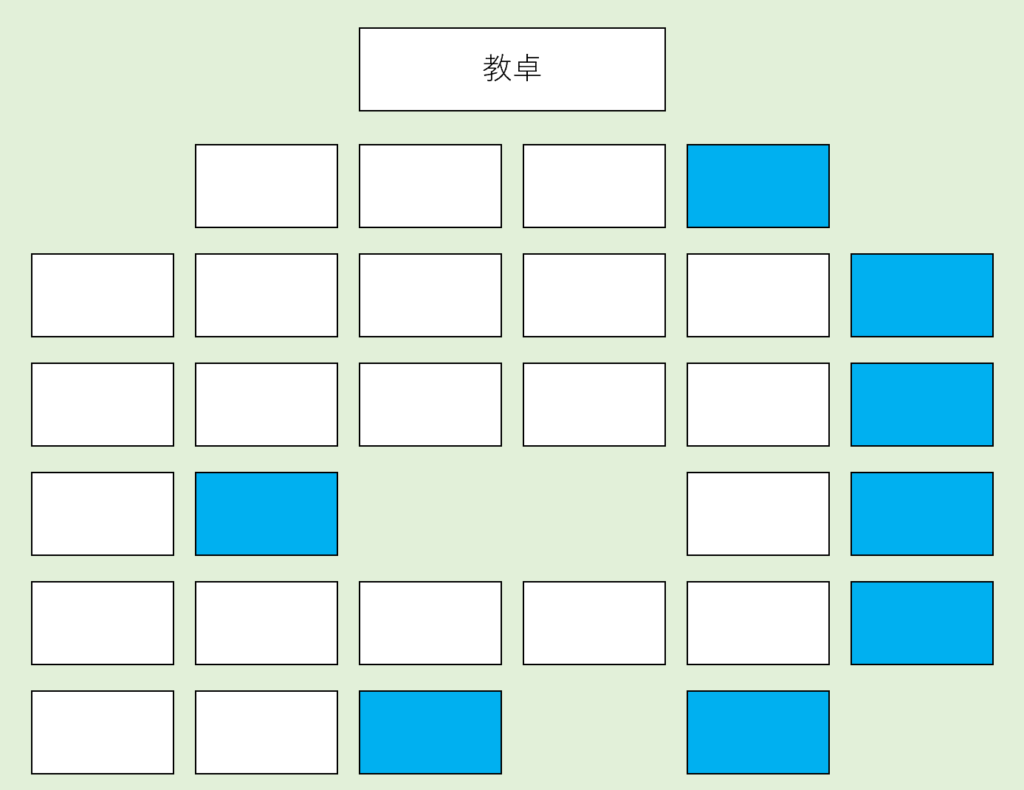
この水色の座席の8個です。
よって座席数は30個なので、\(30 – 8 = 22\) 通りです。
後は同じく「Aさん、Bさん」と「Bさん、Aさん」の2通りずつあるので、隣の座席になる場合の数は \(22 \times 2\) 通りです。
以上から、確率は$$\frac{22 \times 2}{30 \times 29} = \frac{5}{87} = 0.05057‥‥‥=約5\%$$となります。
まとめ:複雑な座席でも簡単に計算できる
いかがでしたでしょうか。
今回の記事をまとめると、次のようになります。
\(n\) 人のクラスで席替えをして、好きな人の隣の座席になる確率は、
右隣がない座席数を \(m\) とすると、$$\frac{(n-m) \times 2}{n(n-1)}$$
どんなに複雑な座席配置でも、右隣がない座席の数を数えるだけで簡単に計算できてしまうのですね!
みなさんも席替えの前に、好きな人の隣に座れる確率を計算してみてはいかがでしょうか。
最後まで読んでいただき、ありがとうございました!
質問やご意見、ご感想などがあればコメント欄にお願いします👇



コメント