【面白い確率】席替えで誰かが同じ席になる確率 | 高校教師とICTのブログ[数学×情報×ICT]

こんにちは。福田泰裕です。

学校生活において、席替えは一大イベントですよね。
「仲良しと近くになりたい…」
「あの子と隣になりたい…」
「後ろの席がいいなぁ…」
など、多くの思いがぶつかり合います。

そんな席替えでも、

〇〇さん、前と同じ席だね！

ということがありませんか？
運が悪かったといえばそれまでなのですが、体感的になかなかの確率で「誰かが同じ席のまま」という事態が発生する気がします。

一体何％くらいの確率で、誰かが同じ席になってしまうのでしょうか？
人数が増えると確率は上がるのでしょうか？それとも下がるのでしょうか？

今回は、席替えをして誰かが同じ席になってしまう確率を考えていきます。

最後まで読んでいただけると嬉しいです。

席替えで「少なくとも1人が同じ席になる確率」を求める

この記事の内容を理解するには、数学Bの数列の知識が必要です。

問題をハッキリさせる

今のままでは問題が曖昧なので、ハッキリさせておきましょう。

$n$ 人の生徒 $ a_1, a_2 , a_3 , \cdots , a_n $ が、
$n$ 個の座席 $ b_1, b_2 , b_3 , \cdots , b_n $ に座っている。
最初の状態では、1以上 $n$ 以下のすべての自然数 $k$ に対して、
生徒 $a_k$ は、座席 $b_k$ に座っているとする。

ここで席替えを行って、生徒と座席の関係をランダムに決める。

ここで、「少なくとも1人が同じ席になる」とは、
「 $a_i = b_i$ となる自然数 $i (1\leq n)$ が存在する」ことである。

分かりやすく言えば、クラスの1回目の席替えをイメージしてください。
最初、生徒は番号順に並んでいますよね？
その机にも同じように番号を付けます。
席替えをした後、出席番号と座席の番号が同じ人がいれば、「少なくとも1人が同じ席になった」ということです。

余事象で考える

このような「少なくとも1人」の問題を考えるときの鉄則です。

「少なくとも1人が同じ席になる」という事は、
「1人が同じ席」「2人が同じ席」「3人が同じ席」……と、かなりの量の計算が待ち受けています。

ということで、「余事象」を考えていきましょう。
「少なくとも1人が同じ席になる」の余事象は「全員が違う席になる」ですね。

まず「全員が違う席になる」確率を求めて、全事象の起こる確率「1」から引き算をする方針で進めていきましょう。

漸化式をつくる

今から考えていく問題は、

$n$ 人の生徒が席替えをしたとき、全員が違う席になる確率

です。
$n$ 人の生徒が $n$ 個の座席へランダムに座るので、この問題の全事象は $n!$ です。
「全員が違う席になる座り方」の場合の数を $f(n)$ 、確率を $P(n)$ とすると、$$P(n)=\frac{f(n)}{n!}$$となります。

まずは $n$ が小さい場合を考えていきます。

$n=1$ のとき、生徒 $a_1$ は絶対に座席 $b_1$ に座るので、違う席に座る座り方はありません。
$f(1)=0$ です。
よって、$P(1)=\frac{f(1)}{1!}=\frac{0}{1}=0$ です。

$n=2$ のとき、2人の生徒の座り方は
① $a_1 , a_2$
② $a_2 , a_1$
の2通りあります。
もとの座席と違うのは、②の場合のみなので $f(2)=1$ です。
よって、$P(2)=\frac{f(2)}{2!}=\frac{1}{2}$ となります。

$n=3$ のとき、3人の生徒の座り方は
① $a_1 , a_2 , a_3$
② $a_1 , a_3 , a_2$
③ $a_2 , a_1 , a_3$
④ $a_2 , a_3 , a_1$
⑤ $a_3 , a_1 , a_2$
⑥ $a_3 , a_2 , a_1$
の6通りです。
全員がもとの座席と違うのは④と⑤の2つなので、$f(3)=2$ です。
よって、$P(3)=\frac{f(3)}{3!}=\frac{2}{3}$ となります。

しかしこの方法だと無限に計算が続くので、漸化式の考え方を利用しましょう。

全員が違う席に座っているとき、生徒 $a_1$ は座席 $b_1$ 以外のどこかに座っていることになります。
例えば、生徒 $a_1$ が座席 $b_k$ に座っているとしましょう。
（※ただし、$(2 \leq k \leq n)$ ）

次に、追い出された生徒 $a_k$ の行方に注目すると、
[ i ]　生徒 $a_k$ が、座席 $b_1$ に座る。
[ ii ]　生徒 $a_k$ が、座席 $b_1$ 以外に座る。
の2つの場合が考えられます。

[ i ]　 $k$ の選び方は $(n-1)$ 通りあります。
生徒 $a_k$が座席 $b_1$ に座っていたとき、座席 $b_1 , b_k$ 以外の $(n-2)$ 個の座席の座り方は $f(n-2)$ 通りです。
よって、この場合の座り方は $(n-1)f(n-2)$ 通りです。

[ ii ]　$k$ の選び方は $(n-1)$ 通りあります。
生徒 $a_k$が座席 $b_1$ 以外に座っていたとき、座席 $a_k$ 以外の $(n-1)$ 個の座席の座り方は $f(n-1)$ 通りです。
よって、この場合の座り方は $(n-1)f(n-1)$ 通りです。

この [ i ] , [ ii ] は同時には起こらないので、
$f(n)=(n-1)f(n-2)+(n-1)f(n-1)$ より、

$f(n)=(n-1)\{f(n-2)+f(n-1)\}$

が成り立ちます。

漸化式を解く

それでは、漸化式

$f(n)=(n-1)\{f(n-2)+f(n-1)\}　,　f(1)=0 , f(2)=1$

を解いていきましょう。

\begin{eqnarray}
f(n) &=& (n-1)f(n-1)+(n-1)f(n-2) \\
&=& nf(n-1)-f(n-1)+(n-1)f(n-2) \\
f(n)-nf(n-1) &=& -\{f(n-1)-(n-1)f(n-2)\}　‥‥‥①
\end{eqnarray}

ここで①の左辺を $g(n)=f(n)-nf(n-1)$ とすると、
①の右辺は $g(n-1)=f(n-1)-(n-1)f(n-2)$ となります。
また、$g(2)=f(2)-2 \cdot f(1)=1-0=1$ なので、

$g(n)=-g(n-1)　,　g(2)=1$

となります。
かなりスッキリしましたね！

この漸化式を続けていくと…
\begin{eqnarray}
g(n)&=&-g(n-1)\\
&=&(-1)^2 g(n-2)\\
&=&(-1)^3 g(n-3)\\
&=& \cdots \\
&=&(-1)^{n-2} g(n-(n-2)) \\
&=& (-1)^{n-2} g(2)\\
&=& (-1)^{n-2}\\
g(n)&=& (-1)^n
\end{eqnarray}

よって、
$f(n)-nf(n-1)=(-1)^n$
という結果が得られました！

次はこの両辺を $n!$ で割ると、
$$\frac{f(n)}{n!}-\frac{f(n-1)}{(n-1)!}=\frac{(-1)^n}{n!}　‥‥‥②$$

「全員が違う席になる」確率は $$P(n)=\frac{f(n)}{n!}$$ なので、②から $$P(n)-P(n-1)=\frac{(-1)^n}{n!}$$となります。

\begin{eqnarray}
P(n)-P(n-1) &=&\frac{(-1)^n}{n!} \\
P(n-1)-P(n-2) &=&\frac{(-1)^{n-1}}{(n-1)!} \\
P(n-2)-P(n-3) &=&\frac{(-1)^{n-2}}{(n-2)!} \\
　\cdots \\
P(2)-P(1) &=&\frac{(-1)^2}{2!} \\
\end{eqnarray}

これらをすべて足すと、
$$P(n)-P(1)=\frac{(-1)^n}{n!}+ \frac{(-1)^{n-1}}{(n-1)!} + \frac{(-1)^{n-2}}{(n-2)!} + \cdots + \frac{(-1)^{2}}{2!} $$
$P(1)=0$ なので、
$$P(n)= \frac{(-1)^n}{n!}+ \frac{(-1)^{n-1}}{(n-1)!} + \frac{(-1)^{n-2}}{(n-2)!} + \cdots + \frac{(-1)^{2}}{2!} $$
つまり、
$$P(n)=\sum_{k=2}^n \frac{(-1)^k}{k!}$$
となります。

これは「全員が違う席になる確率」です。
この余事象を考えると、

$n$ 人が席替えをして「少なくとも1人が同じ席になる」確率は、
$$1- \sum_{k=2}^n \frac{(-1)^k}{k!} $$

となります。

席替えで「少なくとも1人が同じ席になる確率」の考察

この計算結果ではよく分からないので、いろいろと調べてみましょう。

人数ごとの確率

まず、人数によって確率がどのように変わるのかを見ていきましょう。

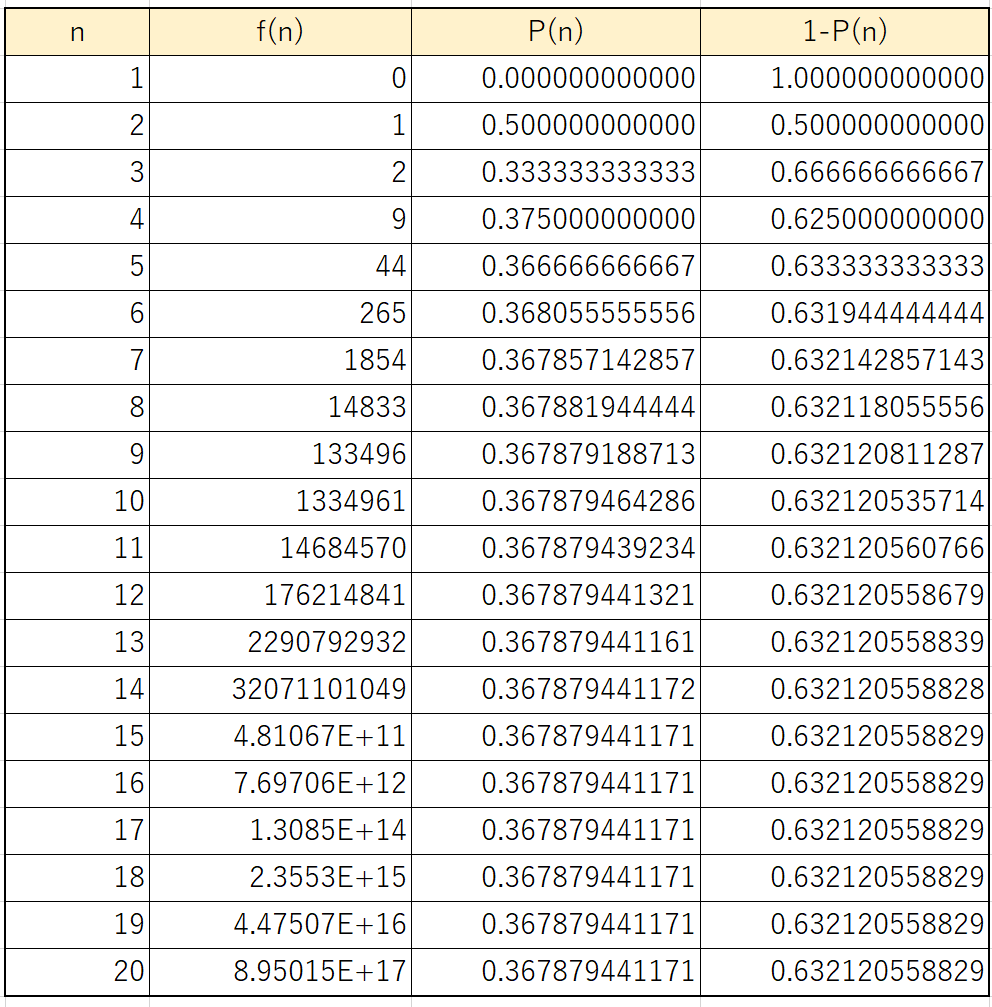
EXCELを使って計算しました。
右端の「1-P(n)」が、「少なくとも1人が同じ席になる確率」です。

見てみると、ある事に気づきませんか？

そうです。
5人以上だとほとんど確率に変化がないのです。
グラフにしてみると、

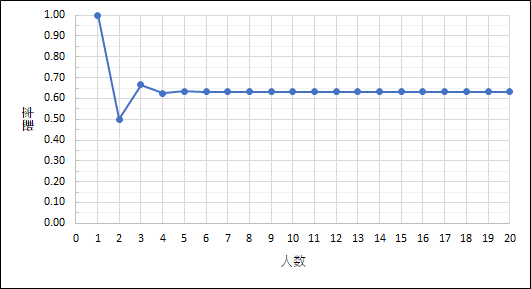
このような形になります。

直感では、人数が増えれば増えるほど同じ席になる確率が下がりそうでしたが、意外な結果となりました！

つまり、席替えをするとき「少なくとも1人が同じ席になる確率」は、5人以上であれば、10人でも、20人でも、40人でも、100人でも、およそ63%と言えるのです！
不思議な結果ですね！

この 0.6321205‥‥‥ という数字は何？

10人以上での確率を見てみると、ずっと
0.6321205‥‥‥
という数字が並んでいます。

これは一体何者でしょうか？

実は先ほどの $$P(n)= \sum_{k=1}^n \frac{(-1)^k}{k!} $$ で、どんどん人数を増やしていき、 $n \to \infty$ の場合を考えてみましょう。
つまり、
$$ \lim_{n \to \infty} P(n) = \lim_{n \to \infty} \sum_{k=1}^n \frac{(-1)^k}{k!} $$ を考えていきます。

突然ですが、数学Ⅲで登場するネイピア数 $e$ というものがあります。
これを $x$ 乗した「 $e^x$ 」をマクローリン展開すると、
$$e^x = 1+x+\frac{x^2}{2!}+ \frac{x^3}{3!}+ \frac{x^4}{4!}+ \cdots$$
となります。

シグマを使うと、
$$e^x = \lim_{n \to \infty} \sum_{k=0}^n \frac{x^k}{k!} $$
と表すことができます。

この式に $x=-1$ を代入すると、
$$e^{-1} = \lim_{n \to \infty} \sum_{k=0}^n \frac{(-1)^k}{k!} $$
つまり、
\begin{eqnarray}
\frac{1}{e} &=& \lim_{n \to \infty} \sum_{k=0}^n \frac{(-1)^k}{k!} \\
&=& \lim_{n \to \infty} P(n)
\end{eqnarray}
となるのです！

つまり「少なくとも1人が同じ席になる確率」の極限は、
$$\lim_{n \to \infty }\{1-P(n)\} = 1- \frac{1}{e}$$
ということになります。

ちなみに、ネイピア数は $e=2.71828 \cdots$ であるから、電卓を使うと
$$\frac{1}{e} = 約37\%$$
となるので、
$$\lim_{n \to \infty}{1- P(n)} = 約67\%$$
となります！